
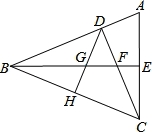
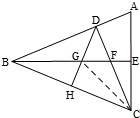
已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.
(1)判断AC与图中的那条线段相等,并证明你的结论;
(2)若CE的长为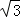 ,求BG的长.
,求BG的长.
【考点】全等三角形的判定与性质;等腰直角三角形.
【分析】(1)根据等腰直角三角形的性质得出BD=CD,根据AAS证明Rt△DFB与Rt△DAC全等即可;
(2)连结CG,利用等腰直角三角形和全等三角形的判定和勾股定理解答即可.
【解答】(1)证明:∵CD⊥AB,
∴∠BDC=90°,
∵∠ABC=45°,
∴△BCD是等腰直角三角形.
∴BD=CD,
∵BE⊥AC于E,
∴∠BEC=90°,
∵∠BFD=∠EFC,
∴∠DBF=∠DCA,
在Rt△DFB与Rt△DAC中,
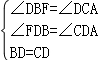 ,
,
∴Rt△DFB≌Rt△DAC,
∴BF=AC;
(2)∵BE平分∠ABC,
∴∠ABE=∠CBE=22.5°,
∵BE⊥AC于E,
∴∠BEA=∠BEC=90°,
又∵BE=BE,
∴Rt△BEA≌Rt△BEC,
∴CE=AE.
连结CG,
∵△BCD是等腰直角三角形,
∴BD=CD,
又H是BC边的中点,
∴DH⊥BC,
∴DH垂直平分BC,
∴BG=CG,
∵∠EBC=22.5°,
∴∠GCB=22.5°,
∴∠EGC=45°,
∴Rt△CEG是等腰直角三角形,
∵CE的长为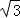 ,
,
∴EG=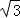 ,
,
利用勾股定理得:CE2+GE2=GC2,
∴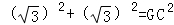 ,
,
∴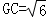 ,
,
∴BG的长为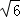 .
.
【点评】本题考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,熟练掌握三角形全等的判定方法并作辅助线构造出全等三角形是解题的关键.


科目:初中数学 来源: 题型:
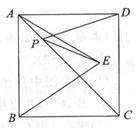
如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为
A.  B. 2
B. 2 C. 2
C. 2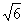 D.
D. 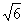
查看答案和解析>>
科目:初中数学 来源: 题型:
2015年是中国人民抗日战争暨世界反法西斯战争胜利70周年.某商家用1200元购进了一批抗战主题纪念衫,上市后果然供不应求,商家又用2800元购进了第二批这种纪念衫,所购数量是第一批购进量的2倍,但单价贵了5元.
(1)该商家购进的第一批纪念衫是多少件?
(2 )若两批纪念衫按相同的标价销售,最后剩下20件按八折优惠卖出,如果两批纪念衫全部售完利润率不低于16%(不考虑其它因素),那么每件纪念衫的标价至少是多少元?
)若两批纪念衫按相同的标价销售,最后剩下20件按八折优惠卖出,如果两批纪念衫全部售完利润率不低于16%(不考虑其它因素),那么每件纪念衫的标价至少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com