练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．将一次函数y=-4x的图象向左平移3个单位，平移后，若y＜4，则x取值范围是x＞-4．

    分析 先利用一次函数平移规律得出平移后解析式，进而解不等式即可求解．

    解答 解：∵将一次函数y=-4x的图象向左平移3个单位，
    ∴平移后解析式为：y=-4（x+3），即y=-4x-12，
    若y＜4，则-4x-12＜4，
    解得x＞-4．
    故答案为x＞-4．

    点评 此题主要考查了一次函数图象与几何变换，掌握“左加右减，上加下减”的平移规律是解题关键．也考查了一元一次不等式的解法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

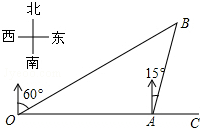    9．如图，港口A在观测站O的正东方向，OA=4km，某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，则该船航行的距离（即AB的长）为2$\sqrt{2}$km．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

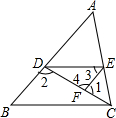    10．如图，已知∠1+∠2=180°，∠3=∠B，
    求证：∠AED=∠ACB，请补充完成下面证明过程．
    证明：∵∠1+∠2=180°（已知）
    ∠1+∠4=180°邻补角的定义
    ∴∠2=∠4（同角的补角相等）
    ∴AB∥EF内错角相等，两直线平行
    ∴∠3=∠AOE（两直线平行，内错角相等）
    ∵∠3=∠B已知
    ∴∠B=∠ADE等量代换
    ∴DE∥BC（同位角相等，两直线平行）
    ∴∠AED=∠ACB两直线平行，同位角相等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列运算中，正确的是（　　）
    A．3a2-a2=2B．（-a2b）3=a6b3C．a3•a6=a9D．（2a2）2=2a4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．先化简，再求值：（$\frac{a}{{a}^{2}-{b}^{2}}$-$\frac{1}{a+b}$）÷$\frac{b}{b-a}$，其中a=-1+$\sqrt{2}$，b=1+$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

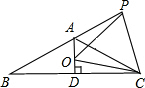    4．已知如图等腰△ABC，AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，
    （1）证明：∠APO+∠DCO=30°；
    （2）判断△OPC的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

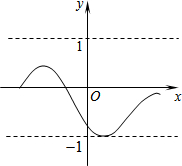    11．对某一个函数给出如下定义：若存在实数M＞0，对于任意的函数值y，都满足-M≤y≤M，则称这个函数是有界函数，在所有满足条件的M中，其最小值称为这个函数的边界值．例如，图中的函数是有界函数，其边界值1．若函数y=-x+1（a≤x≤b，b＞a）的边界值是2，且这个函数的最大值也是2，则b的取值范围是-1＜b≤3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．先化简，然后再选一个合适的x值代入，求值：$（\frac{x+2}{{{x^2}-2x}}-\frac{x-1}{{{x^2}-4x+4}}）÷\frac{{{x^2}-16}}{{{x^2}+4x}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．下列各运算中，计算正确的是（　　）
    A．3x2+5x2=8x4B．$\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$
    C．$\frac{1}{x+1}$-$\frac{1}{x-1}$=$\frac{2}{{{x^2}-1}}$D．（-$\frac{1}{2}$m2n）2=$\frac{1}{4}$m4n2

    查看答案和解析>>

    同步练习册答案