
【题目】设函数y=k1x+![]() ,且k1k2≠0,自变量x与函数值y满足以下表格:
,且k1k2≠0,自变量x与函数值y满足以下表格:
x | …… | -4 | -3 | -2 | -1 | - |
| 1 | 2 | 3 | 4 | …… |
y | …… | -3 | -2 | -1 | 0 | 1 | -1 | 0 | 1 | m | n | …… |
(1)根据表格直接写出y与x的函数表达式及自变量x的取值范围______
(2)补全上面表格:m=______,n=______;在如图所示的平面直角坐标系中,请根据表格中的数据补全y关于x的函数图象;
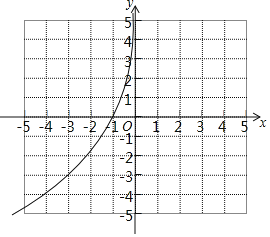
(3)结合函数图象,解决下列问题:
①写出函数y的一条性质:______;
②当函数值y≥![]() 时,x的取值范围是______;
时,x的取值范围是______;
③当函数值y=-x时,结合图象请估算x的值为______(结果保留一位小数)
【答案】(1)y=x-![]() (x≠0);(2)2
(x≠0);(2)2![]() ,3
,3![]() ;(3)①当x≥1时,y随x的增大而增大;②x=-
;(3)①当x≥1时,y随x的增大而增大;②x=-![]() 或x≥2;③±0.7
或x≥2;③±0.7
【解析】
(1)把(-1,0),(2,1![]() )代入y=k1x+
)代入y=k1x+![]() 解方程组即可得到结论;
解方程组即可得到结论;
(2)当x=3时,当x=4时,定义函数解析式即可得到结论;补全y关于x的函数图象即可;
(3)根据函数图象即可得到结论.
解:(1)把(-1,0),(2,1![]() )代入y=k1x+
)代入y=k1x+![]() 得,
得,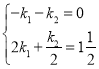 ,
,
解得: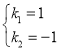 ,
,
∴y与x的函数表达式为:y=x-![]() (x≠0);
(x≠0);
故答案为:y=x-![]() (x≠0);
(x≠0);
(2)当x=3时,m=3-![]() =2
=2![]() ,当x=4时,n=4-
,当x=4时,n=4-![]() =3
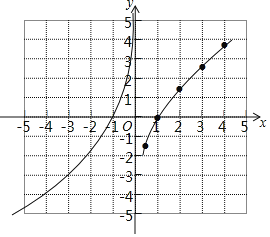
=3![]() ;补全y关于x的函数图象如图所示;
;补全y关于x的函数图象如图所示;
故答案为:2![]() ,3
,3![]() ;
;
(3)由图象知,①当x≥1时,y随x的增大而增大;
②当函数值y≥![]() 时,x的取值范围是:x=-
时,x的取值范围是:x=-![]() 或x≥2;
或x≥2;
③当函数值y=-x时,结合图象请估算x的值为±0.7,
故答案为:当x≥1时,y随x的增大而增大;x=-![]() 或x≥2;±0.7.
或x≥2;±0.7.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】(阅读材料)
性质:在一个三角形中,各边和它所对角的正弦的比相等.
即:![]()
利用上述性质可以求解如下题目:
在![]() 中,若
中,若![]() ,
,![]() ,
,![]() ,求b.
,求b.
解:在![]() 中,∵
中,∵![]() ,
,
∴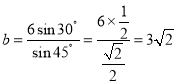 .
.
(问题解决)利用上述相关知识解决下列问题:
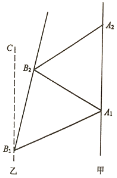
如图,甲船以每小时![]() 海里的速度向正北方向航行.当甲船位于
海里的速度向正北方向航行.当甲船位于![]() 处时,乙船位于甲船的南偏西
处时,乙船位于甲船的南偏西![]() 方向的
方向的![]() 处,且乙船从
处,且乙船从![]() 处沿北偏东
处沿北偏东![]() 方向匀速直线航行.经过20分钟后,甲船由
方向匀速直线航行.经过20分钟后,甲船由![]() 处航行到
处航行到![]() 处,乙船航行到甲船位置(即
处,乙船航行到甲船位置(即![]() 处)的南偏西
处)的南偏西![]() 方向的
方向的![]() 处,此时两船相距
处,此时两船相距![]() 海里,求乙船每小时航行多少海里.
海里,求乙船每小时航行多少海里.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两人分别从![]() ,
,![]() 两地相向而行,甲先走3分钟后乙才开始行走,甲到达
两地相向而行,甲先走3分钟后乙才开始行走,甲到达![]() 地后立即停止,乙到达
地后立即停止,乙到达![]() 地后立即以另一速度返回
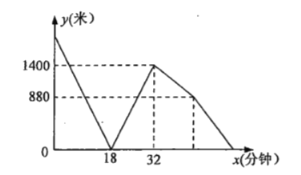
地后立即以另一速度返回![]() 地,在整个行驶的过程中,两人保持各自速度匀速行走,甲,乙两人之间的距离
地,在整个行驶的过程中,两人保持各自速度匀速行走,甲,乙两人之间的距离![]() (米)与乙出发的时间
(米)与乙出发的时间![]() (分钟)的函数关系如图所示.当甲到达
(分钟)的函数关系如图所示.当甲到达![]() 地时,则乙距离
地时,则乙距离![]() 地的时间还需要________分钟.
地的时间还需要________分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程2x2+2x﹣1=0的两个根为x1,x2,且x1<x2,下列结论正确的是( )
A. x1+x2=1 B. x1x2=﹣1 C. |x1|<|x2| D. x12+x1=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东坡商贸公司购进某种水果成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价P(元/kg)与时间t(天)之间的函数关系式P=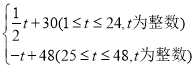 且其日销售量y(kg)与时间t(天)的关系如表下:
且其日销售量y(kg)与时间t(天)的关系如表下:
时间t(天) | 1 | 3 | 6 | 10 | 20 | … |
日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | … |
(1)已知y与t之间的变化符合一次函数关系,试求在第30天的日销售量.
(2)哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售前24天中,该公司决定每销售1kg水果就捐赠n元利润(0<n<9)给“精准扶贫”对象,现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD中,![]() ,点E是BC边上的一点(不与B,C重合),以BE为边构造菱形BEFG,使点G落在AB的延长线上,连接BD,GE,射线FE交BD于点H.
,点E是BC边上的一点(不与B,C重合),以BE为边构造菱形BEFG,使点G落在AB的延长线上,连接BD,GE,射线FE交BD于点H.
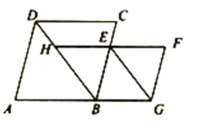
(1)求证:四边形BGEH是平行四边形;
(2)请从下面AB两题中任选一题作答,我选择______题.
A.若四边形BGEH为菱形,则BD的长为_____.
B.连接HC,CF,BF,若![]() ,且四边形BHCF为矩形,则CF的长为______.
,且四边形BHCF为矩形,则CF的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点.
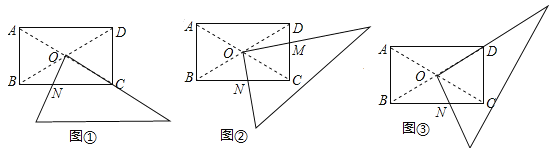
(1)该学习小组成员意外的发现图①中(三角板一边与CC重合),BN、CN、CD这三条线段之间存在一定的数量关系:CN2=BN2+CD2,请你对这名成员在图①中发现的结论说明理由;
(2)在图③中(三角板一直角边与OD重合),试探究图③中BN、CN、CD这三条线段之间的数量关系,直接写出你的结论.
(3)试探究图②中BN、CN、CM、DM这四条线段之间的数量关系,写出你的结论,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com