
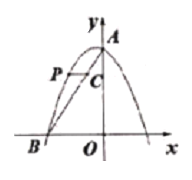
【题目】如图,二次函数y=-x2+(n-1)x+3的图像与y轴交于点A,与x轴的负半轴交于点B(-2,0)
(1)求二次函数的解析式;
(2)点P是这个二次函数图像在第二象限内的一线,过点P作y轴的垂线与线段AB交于点C,求线段PC长度的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)将点B坐标代入即可求出解析式;
(2)先求出直线AB的解析式为![]() ,设点P的坐标为(x,
,设点P的坐标为(x,![]() ),则点C的坐标为(
),则点C的坐标为(![]() ,
,![]() ),列出线段PC的关系式配方即可得到PC的最大值.
),列出线段PC的关系式配方即可得到PC的最大值.
(1)将点B(-2,0)代入y=-x2+(n-1)x+3中,得-4-2(n-1)+3=0,
解得n=![]() ,
,
∴![]() ;
;
(2)当x=0时得y=3,
∴A(0,3),
设直线AB的解析式为y=kx+b,
![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为![]() ,
,
设点P的坐标为(x,![]() ),由题意可知点C的纵坐标是
),由题意可知点C的纵坐标是![]() ,代入
,代入![]() ,则可得点C的坐标为(
,则可得点C的坐标为(![]() ,
,![]() ),
),
因为C在P的右侧,
∴PC=![]() =
=![]() ,
,
因为点P是这个二次函数图像在第二象限内的一点,所以![]() ,
,
∴当![]() 时,PC长度的最大值是
时,PC长度的最大值是![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,点D是边BC上的动点,连接AD,点C关于直线AD的对称点为点E,射线BE与射线AD交于点F.


(1)在图1中,依题意补全图形;
(2)记![]() (
(![]() ),求
),求![]() 的大小;(用含
的大小;(用含![]() 的式子表示)
的式子表示)
(3)若△ACE是等边三角形,猜想EF和BC的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,∠BAD =90°,AC是对角线.点E在BC的延长线上,且∠CED =∠BAC.
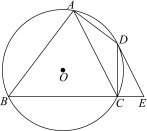
(1)判断DE与⊙O的位置关系,并说明理由;
(2)BA与CD的延长线交于点F,若DE∥AC,AB=4,AD =2,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+2ax-3与x轴交于A、B(1,0)两点(点A在点B的左侧),与y轴交于点C,将抛物线沿y轴平移m(m>0)个单位,当平移后的抛物线与线段OA有且只有一个交点时,则m的取值范围是_______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知矩形ABCD,AB=4,AD=3,点E为边DC上不与端点重合的一个动点,连接BE,将BCE沿BE翻折得到BEF,连接AF并延长交CD于点G,则线段CG的最大值是( )
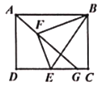
A.1B.1.5C.4-![]() D.4-
D.4-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】题目:为了美化环境,某地政府计划对辖区内![]() 的土地进行绿化.为了尽快完成任务,实际平均每月的绿化面积是原计划的1.5倍,结果提前2个月完成任务.求原计划平均每月的绿化面积.
的土地进行绿化.为了尽快完成任务,实际平均每月的绿化面积是原计划的1.5倍,结果提前2个月完成任务.求原计划平均每月的绿化面积.
甲同学所列的方程为![]()
乙同学所列的方程为![]()
(1)甲同学所列的方程中![]() 表示 .乙同学所列的方程中
表示 .乙同学所列的方程中![]() 表示 .
表示 .
(2)任选甲、乙两同学的其中一个方法解答这个题目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,在![]() 和
和![]() 中,
中,![]() ,连接
,连接![]() 交于点
交于点![]() .求证:
.求证:![]() ;并直接写出
;并直接写出![]() ______.
______.
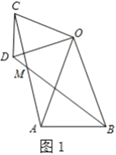
(2)类比探究:如图2,在![]() 和
和![]() 中,
中,![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() .请判断
.请判断![]() 的值及
的值及![]() 的度数.
的度数.
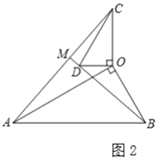
(3)拓展延伸:在(2)的条件下,将![]() 绕点
绕点![]() 在平面内旋转,
在平面内旋转,![]() 所在直线
所在直线![]() 交于点.若
交于点.若![]() ,请直接写出当点
,请直接写出当点![]() 与点
与点![]() 重合时
重合时![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.
(1)甲组抽到A小区的概率是多少;
(2)请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com