练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

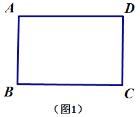
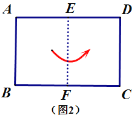
    【题目】如图1，矩形纸片满足．将此矩形纸片按下列顺序折叠，则图4中的长为___________________(用含的代数式表示)．

    【答案】

    【解析】

    如下图，利用折叠和矩形的特点得出△EIG是等腰直角三角形，同样得出△EJM是等腰直角三角形，然后推导出EJ的长，便可得MJ的长，从而得出MN的长．

    根据题意，图形如下

    ∵矩形ABCD中，

    ∴AE=GI=BF=，∠A=90°

    ∵△GEI是△GEA折叠得到

    ∴EI=AE==GI，∠EIG=90°，

    ∴IF=

    ∴△GIE是等腰直角三角形，

    ∴∠IEG=45°

    ∵∠EFB=90°，

    ∴∠EJ=90°

    ∴△EJM是等腰直角三角形

    ∵IF=，

    ∴JI=，

    ∴JE=

    ∴在等腰直角△EJM中，JM=

    ∴MN=

    故答案为：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

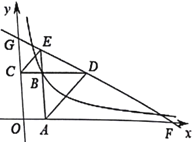
    【题目】如图，矩形OABC在直角坐标系中，延长AB至点E使得BE=BC连接CE，过A作AD//CE交CB延长线于点D，直线DE分别交x轴、y轴于F、G点，若EG：DF=1：4，且△BCE与△BAD面积之和为，则过点的双曲线中的值为____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某工厂制作两种手工艺品，每天每件获利比多105元，获利30元的与获利240元的数量相等．

    （1）制作一件和一件分别获利多少元？

    （2）工厂安排65人制作，两种手工艺品，每人每天制作2件或1件．现在在不增加工人的情况下，增加制作．已知每人每天可制作1件（每人每天只能制作一种手工艺品），要求每天制作，两种手工艺品的数量相等．设每天安排人制作，人制作，写出与之间的函数关系式．

    （3）在（1）（2）的条件下，每天制作不少于5件．当每天制作5件时，每件获利不变．若每增加1件，则当天平均每件获利减少2元．已知每件获利30元，求每天制作三种手工艺品可获得的总利润（元）的最大值及相应的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

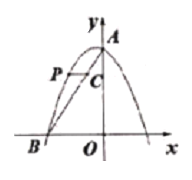
    【题目】如图，二次函数y=-x2+(n-1)x+3的图像与y轴交于点A，与x轴的负半轴交于点B(-2，0)

    (1)求二次函数的解析式；

    (2)点P是这个二次函数图像在第二象限内的一线，过点P作y轴的垂线与线段AB交于点C，求线段PC长度的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】游泳池换水清洗的整个过程为“排水-清洗-注水”．一个长方体的游泳池在一次换水清洗的过程中，排水速度是注水速度的2倍，清洗的时间为，这次换水清洗过程中游泳池水量与时间之间的函数图像如图所示．

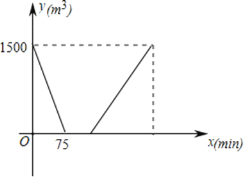
    （1）这次换水清洗的过程中排水的速度为 ．

    （2）求“注水”过程中与之间的函数关系式，并写出自变量的取值范围．

    （3）在该游泳池换水清洗的整个过程中，当池水的水位高度恰好是注满水的池中水位高度的时，直接写出的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，点在上，且．动点同时从点出发，均以的速度运动，其中点P沿向终点运动；点沿向终点运动．过点作分交于点，设动点运动的时间为秒．

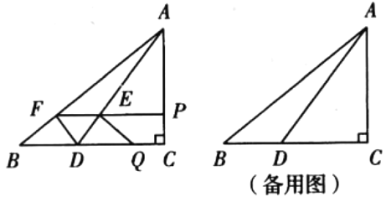
    （1）求的长(用含的代数式表示)；

    （2）以点为顶点圈成的围形面积为求与之间的函数关系式；

    （3）连接若点为中点在整个运动过程中，直接写出点运动的路径长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，大正方形中，，小正方形中，，在小正方形绕点旋转的过程中，当时，线段的长为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】国内猪肉价格不断上涨，已知今年10月的猪肉价格比今年年初上涨了80%，李奶奶10月在某超市购买1千克猪肉花了72元钱．

    （1）今年年初猪肉的价格为每千克多少元？

    （2）某超市将进货价为每千克55元的猪肉按10月价格出售，平均一天能销售出100千克，随着国家对猪肉价格的调控，超市发现猪肉的售价每千克下降1元，其日销售量就增加10千克，超市为了实现销售猪肉每天有1800元的利润，并且尽可能让顾客得到实惠，猪肉的售价应该下降多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知如图所示的抛物线顶点的坐标为，且过点．

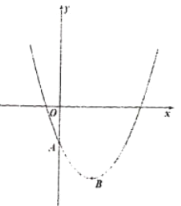
    （1）求该抛物线的解析式；

    （2）若点为抛物线对称轴右侧、轴下方一点，当时，求直线的解析式；

    （3）平移（1）中的抛物线，记平移后抛物线的顶点为，顶点在直线上滑动，且平移后的抛物线与直线交于另一点，若点为平移前（1）中抛物线上的点，则当以、、三点为顶点的三角形是等腰直角三角形时，求出所有符合条件的点的坐标．

    查看答案和解析>>

    同步练习册答案