
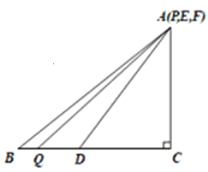
【题目】如图,在![]() 中,
中,![]() 点
点![]() 在
在![]() 上,且
上,且![]() .动点
.动点![]() 同时从点
同时从点![]() 出发,均以
出发,均以![]() 的速度运动,其中点P沿
的速度运动,其中点P沿![]() 向终点
向终点![]() 运动;点
运动;点![]() 沿
沿![]() 向终点
向终点![]() 运动.过点
运动.过点![]() 作
作![]() 分交
分交![]() 于点
于点![]() ,设动点
,设动点![]() 运动的时间为
运动的时间为![]() 秒.
秒.
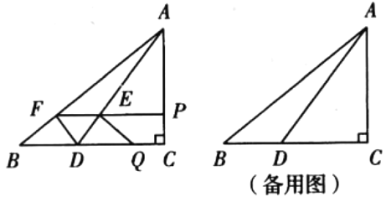
(1)求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)以点![]() 为顶点圈成的围形面积为
为顶点圈成的围形面积为![]() 求
求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)连接![]() 若点
若点![]() 为
为![]() 中点在整个运动过程中,直接写出点
中点在整个运动过程中,直接写出点![]() 运动的路径长.
运动的路径长.
【答案】(1)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;(2)
;(2)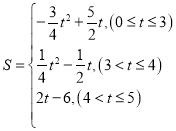 ;(3)
;(3)![]()
【解析】
(1)直接根据题意可判断DQ的长度;
(2)需要分3种情况分析,一种是当![]() 时,此段点Q在点D的右侧;第二种是当
时,此段点Q在点D的右侧;第二种是当![]() 时,此段点Q在点D左侧,点P还未到达点A;第三段是当
时,此段点Q在点D左侧,点P还未到达点A;第三段是当![]() 时,此段点P到达点A处,点Q在DB上运动;
时,此段点P到达点A处,点Q在DB上运动;
(3)需要分2段考虑,一段是![]() 时,此段,点P在CA上运动,点Q在CB上运动;第二段是
时,此段,点P在CA上运动,点Q在CB上运动;第二段是![]() 时,此段,点P到达点A处,点Q在DB上运动.
时,此段,点P到达点A处,点Q在DB上运动.
(1)根据题意:
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
(2)![]() 当
当![]() 时,如下图:
时,如下图:
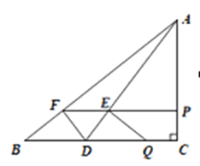
![]()
![]()
![]()
![]()
![]()
![]() 当
当![]() 时,如下图:
时,如下图:
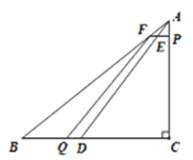
![]()
![]() 当
当![]() 时,如下图:
时,如下图:
![]()
综上所述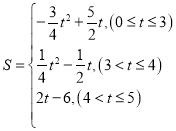
(3)如下图,在BC上取点G,使得GC=4,取AG、AB的中点为T、N,连接CM,TN
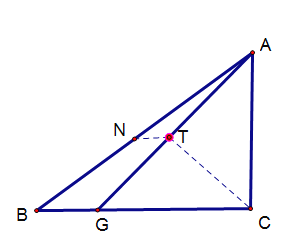
![]() 当0≤t≤4时
当0≤t≤4时
点P在CA上运动,点Q在CG上运动,当t=4时,点P运动到点A处,点Q运动到点G处
∵点M是PQ的中点
∴在此段运动过程中,点M的运动轨迹为CT
∵AC=CG=4,∠ACG=90°,点T是AG的中点
∴CT=2![]()
b.当4<t≤5时
点P到达点A处,点Q在GB上运动,直至到达点B
∵点M是PQ的中点
∴当t=5时,点M在点N处,即AB的中点
故在此段运动过程中,点M的运动轨迹为TN
∵点T、N分别时AG、AB的中点
∴TN是△ABG的中位线
∵BC=5,CG=4
∴GB=1
∴TN=![]()
∴点M在整个过程中的路程为:2![]()


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:
对于任意正实数a、b,
∵![]() ,
,
![]()
![]() 当且仅当
当且仅当![]() 时,等号成立.
时,等号成立.
结论:在![]() 均为正实数)中,若
均为正实数)中,若![]() 为定值
为定值![]() 则
则![]() 当且仅当
当且仅当![]() 时,a+b有最小值
时,a+b有最小值![]() .
.
拓展:对于任意正实数![]() ,都有
,都有![]() 当且仅当
当且仅当![]() 时,等号成立.
时,等号成立.
在![]() (a、b、c均为正实数)中,若
(a、b、c均为正实数)中,若![]() 为定值
为定值![]() ,则
,则![]() 当且仅当
当且仅当![]() 时,
时,![]() 有最小值
有最小值![]()
例如:![]() 则
则![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
又如:若![]() 求
求![]() 的最小值时,因为
的最小值时,因为![]() 当且仅当
当且仅当![]() ,即
,即![]() 时等号成立,故当
时等号成立,故当![]() 时,
时,![]() 有最小值
有最小值![]() .
.
根据上述材料,解答下列问题:
(1)若a为正数,则当a=______时,代数式![]() 取得最小值,最小值为_____;
取得最小值,最小值为_____;
(2)已知函数![]() 与函数
与函数![]() ,求函数
,求函数![]() 的最小值及此时
的最小值及此时![]() 的值;
的值;
(3)我国某大型空载机的一次空载运输成本包含三部分:一是基本运输费用,共8100元;二是飞行耗油,每一百公里1200元;三是飞行报耗费用,飞行报耗费用与路程(单位:百公里)的平方成正比,比例系数为0.04,设该空载机的运输路程为![]() 百公里,则该空载机平均每一百公里的运输成本
百公里,则该空载机平均每一百公里的运输成本![]() 最低为多少?
最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+2ax-3与x轴交于A、B(1,0)两点(点A在点B的左侧),与y轴交于点C,将抛物线沿y轴平移m(m>0)个单位,当平移后的抛物线与线段OA有且只有一个交点时,则m的取值范围是_______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】题目:为了美化环境,某地政府计划对辖区内![]() 的土地进行绿化.为了尽快完成任务,实际平均每月的绿化面积是原计划的1.5倍,结果提前2个月完成任务.求原计划平均每月的绿化面积.
的土地进行绿化.为了尽快完成任务,实际平均每月的绿化面积是原计划的1.5倍,结果提前2个月完成任务.求原计划平均每月的绿化面积.
甲同学所列的方程为![]()
乙同学所列的方程为![]()
(1)甲同学所列的方程中![]() 表示 .乙同学所列的方程中
表示 .乙同学所列的方程中![]() 表示 .
表示 .
(2)任选甲、乙两同学的其中一个方法解答这个题目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与直线
两点,与直线![]() 交于
交于![]() 、
、![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
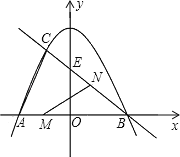
(1)求直线![]() 的解析式:
的解析式:
(2)若点![]() 在线段
在线段![]() 上以每秒1个单位长度的速度从点
上以每秒1个单位长度的速度从点![]() 向点
向点![]() 运动(不与点
运动(不与点![]() 、
、![]() 重合),同时,点
重合),同时,点![]() 在射线
在射线![]() 上以每秒2个单位长度的速度从点
上以每秒2个单位长度的速度从点![]() 向点
向点![]() 方向运动,设运动的时间为
方向运动,设运动的时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求
的函数关系式,并求![]() 取何值时,
取何值时,![]() 最大?最大值是多少?
最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
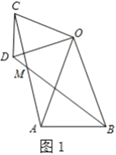
【题目】(1)问题发现:如图1,在![]() 和
和![]() 中,
中,![]() ,连接
,连接![]() 交于点
交于点![]() .求证:
.求证:![]() ;并直接写出
;并直接写出![]() ______.
______.
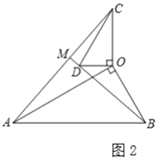
(2)类比探究:如图2,在![]() 和
和![]() 中,
中,![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() .请判断
.请判断![]() 的值及
的值及![]() 的度数.
的度数.
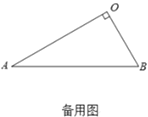
(3)拓展延伸:在(2)的条件下,将![]() 绕点
绕点![]() 在平面内旋转,
在平面内旋转,![]() 所在直线
所在直线![]() 交于点.若
交于点.若![]() ,请直接写出当点
,请直接写出当点![]() 与点
与点![]() 重合时
重合时![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为防控“新型冠状病毒”,某超市分别用1600元、6000元购进两批防护口罩,第二批防护口罩的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批口罩进货单价多少元?
(2)若这两次购买防护口罩过程中所产生其他费用不少于600元,那么该超市购买这两批防护口罩的平均单价至少为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com