
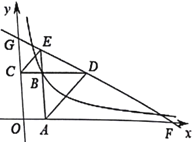
【题目】如图,矩形OABC在直角坐标系中,延长AB至点E使得BE=BC连接CE,过A作AD//CE交CB延长线于点D,直线DE分别交x轴、y轴于F、G点,若EG:DF=1:4,且△BCE与△BAD面积之和为![]() ,则过点
,则过点![]() 的双曲线
的双曲线![]() 中
中![]() 的值为____.
的值为____.
【答案】3
【解析】
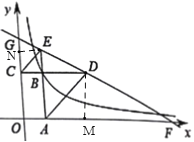
如图,过点E作EN⊥y轴于N,过点D作DM⊥x轴于M,设B(x、y),由矩形的性质及BE=BC可得△BCE是等腰直角三角形,可得∠BCE=45°,根据平行线的性质可得∠ADC=∠BCE=45°,可得△ABD是等腰直角三角形,可得BD=AB=y,根据平行线的性质可得∠NEG=∠BDE=∠MFD,可证明△NEG∽△MFD,△BDE∽△MFD,根据相似三角形的性质可得y2=4x2,根据△BCE与△BAD面积之和为![]() 可得x2+y2=
可得x2+y2=![]() ,进而求出xy的值即可得答案.
,进而求出xy的值即可得答案.
如图,过点E作EN⊥y轴于N,过点D作DM⊥x轴于M,设B(x、y),
∴BC=x,AB=y,
∵BE=BC,四边形OABC是矩形,
∴△BCE是等腰直角三角形,
∴∠BCE=45°,
∵AD//CE,
∴∠ADC=∠BCE=45°,
∴△ABD是等腰直角三角形,
∴BD=AB=y,
∵EN⊥y轴,DM⊥x轴,
∴四边形GCBE、BAMD都是正方形,
∴EG=BC=x,DM=AB=y,
∵∠GNE=∠DCG=∠FOG=90°,
∴EG//CD//OF,
∴∠NEG=∠BDE=∠MFD,
∴△NEG∽△MFD,△BDE∽△MFD,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴y2=4x2,
∵△BCE与△BAD面积之和为![]() ,
,
∴![]() x2+
x2+![]() y2=
y2=![]() ,即x2+y2=
,即x2+y2=![]() ,
,
∴x2+4x2=![]() ,
,
解得:x2=![]() ,
,
∴y2=4x2=6,
∴(xy)2=9,
∵点B在双曲线![]() 图象上,且图象在第一象限,
图象上,且图象在第一象限,
∴k=xy=3,
故答案为:3


科目:初中数学 来源: 题型:
【题目】若一个两位数中,个位数字比十位数字大1,则称这个两位数为“递增数”.例如56就是一个“递增数”,现有2,3,4,5四个数字.
(1)若先抽出的数字3作为十位数,再从其余3个数字随机抽出1个数字为个位数,组成的两位数恰为“递增数”的概率为________.
(2)先从四个数中随机抽出一个数作为十位数,再从其余3个数字随机抽出1个数字为个位数.组成的两位数恰为“递增数”的概率是多少?请用列表或画树状图的方法分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上一动点(与点
边上一动点(与点![]() 不重合),连接
不重合),连接![]() 将
将![]() 的两边所在射线
的两边所在射线![]() 以点
以点![]() 为中心,顺时针旋转
为中心,顺时针旋转![]() 分别交射线
分别交射线![]() 于点
于点![]() .
.
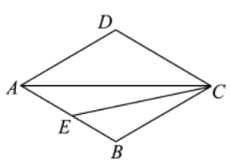
(1)依题意补全图形;
(2)若![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示) ;
的式子表示) ;
(3)用等式表示线段![]() 与
与![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,点D是边BC上的动点,连接AD,点C关于直线AD的对称点为点E,射线BE与射线AD交于点F.


(1)在图1中,依题意补全图形;
(2)记![]() (
(![]() ),求
),求![]() 的大小;(用含
的大小;(用含![]() 的式子表示)
的式子表示)
(3)若△ACE是等边三角形,猜想EF和BC的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 上一动点,以
上一动点,以![]() 为顶点,且经过原点
为顶点,且经过原点![]() 的抛物线,记作“
的抛物线,记作“![]() ”,设其与
”,设其与![]() 轴另一交点为
轴另一交点为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() .
.
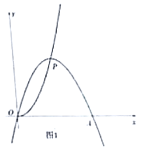
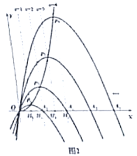
(1)①当![]() 为直角三角形时,
为直角三角形时,![]() ________;
________;
②当![]() 为等边三角形时,求此时“
为等边三角形时,求此时“![]() ”的解析式;
”的解析式;
(2)若![]() 点的横坐标分别为1,2,3,……
点的横坐标分别为1,2,3,……![]() (
(![]() 为正整数)时,抛物线“
为正整数)时,抛物线“![]() ”,分别记作“
”,分别记作“![]() ”,“
”,“![]() ”…“
”…“![]() ”,设其与
”,设其与![]() 轴另一交点分别为
轴另一交点分别为![]() ,
,![]() ,
,![]() …
…![]() ,过
,过![]() ,
,![]() ,
,![]() ,…,
,…,![]() 作
作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,
,![]() ,
,![]() ,…,
,…,![]() .
.
①![]() 的坐标为________,
的坐标为________,![]() ________;(用含
________;(用含![]() 的代数式表示)
的代数式表示)
②当![]() 时,求
时,求![]() 的值;
的值;
③是否存在这样的![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
对于任意正实数a、b,
∵![]() ,
,
![]()
![]() 当且仅当
当且仅当![]() 时,等号成立.
时,等号成立.
结论:在![]() 均为正实数)中,若
均为正实数)中,若![]() 为定值
为定值![]() 则
则![]() 当且仅当
当且仅当![]() 时,a+b有最小值
时,a+b有最小值![]() .
.
拓展:对于任意正实数![]() ,都有
,都有![]() 当且仅当
当且仅当![]() 时,等号成立.
时,等号成立.
在![]() (a、b、c均为正实数)中,若
(a、b、c均为正实数)中,若![]() 为定值
为定值![]() ,则
,则![]() 当且仅当
当且仅当![]() 时,
时,![]() 有最小值
有最小值![]()
例如:![]() 则
则![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
又如:若![]() 求
求![]() 的最小值时,因为
的最小值时,因为![]() 当且仅当
当且仅当![]() ,即
,即![]() 时等号成立,故当
时等号成立,故当![]() 时,
时,![]() 有最小值
有最小值![]() .
.
根据上述材料,解答下列问题:
(1)若a为正数,则当a=______时,代数式![]() 取得最小值,最小值为_____;
取得最小值,最小值为_____;
(2)已知函数![]() 与函数
与函数![]() ,求函数
,求函数![]() 的最小值及此时
的最小值及此时![]() 的值;
的值;
(3)我国某大型空载机的一次空载运输成本包含三部分:一是基本运输费用,共8100元;二是飞行耗油,每一百公里1200元;三是飞行报耗费用,飞行报耗费用与路程(单位:百公里)的平方成正比,比例系数为0.04,设该空载机的运输路程为![]() 百公里,则该空载机平均每一百公里的运输成本
百公里,则该空载机平均每一百公里的运输成本![]() 最低为多少?
最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线![]() (
(![]() 、
、![]() 为常数)的顶点为
为常数)的顶点为![]() ,等腰直角三角形
,等腰直角三角形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,
,![]() 的坐标为
的坐标为![]() ,直角顶点
,直角顶点![]() 在第四象限.
在第四象限.
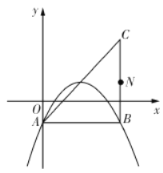
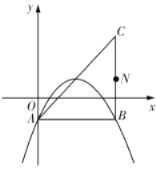
(1)如图,若该抛物线经过![]() 、
、![]() 两点,求该抛物线的函数表达式;
两点,求该抛物线的函数表达式;
(2)平移(1)中的抛物线,使顶点![]() 在直线
在直线![]() 上滑动,且与
上滑动,且与![]() 交于另一点
交于另一点![]() .
.
①若点![]() 在直线
在直线![]() 下方,且为平移前(1)中的抛物线上的点,当以
下方,且为平移前(1)中的抛物线上的点,当以![]() 、
、![]() 、
、![]() 三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点
三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点![]() 的坐标;
的坐标;
②取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,∠BAD =90°,AC是对角线.点E在BC的延长线上,且∠CED =∠BAC.
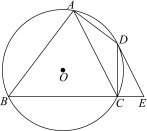
(1)判断DE与⊙O的位置关系,并说明理由;
(2)BA与CD的延长线交于点F,若DE∥AC,AB=4,AD =2,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com