
ЎѕМвДїЎїФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬ТСЦЄЕЧОпПЯ![]() ЈЁ
ЈЁ![]() Ўў
Ўў![]() ОЄіЈКэЈ©µД¶ҐµгОЄ
ОЄіЈКэЈ©µД¶ҐµгОЄ![]() Ј¬µИСьЦ±ЅЗИэЅЗРО
Ј¬µИСьЦ±ЅЗИэЅЗРО![]() µД¶Ґµг
µД¶Ґµг![]() µДЧш±кОЄ
µДЧш±кОЄ![]() Ј¬
Ј¬![]() µДЧш±кОЄ
µДЧш±кОЄ![]() Ј¬Ц±ЅЗ¶Ґµг
Ј¬Ц±ЅЗ¶Ґµг![]() ФЪµЪЛДПуПЮЈ®
ФЪµЪЛДПуПЮЈ®
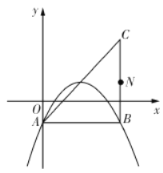
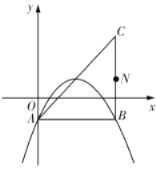
ЈЁ1Ј©ИзНјЈ¬ИфёГЕЧОпПЯѕ№э![]() Ўў
Ўў![]() БЅµгЈ¬ЗуёГЕЧОпПЯµДєЇКэ±нґпКЅЈ»
БЅµгЈ¬ЗуёГЕЧОпПЯµДєЇКэ±нґпКЅЈ»
ЈЁ2Ј©ЖЅТЖЈЁ1Ј©ЦРµДЕЧОпПЯЈ¬К№¶Ґµг![]() ФЪЦ±ПЯ
ФЪЦ±ПЯ![]() ЙП»¬¶ЇЈ¬ЗТУл
ЙП»¬¶ЇЈ¬ЗТУл![]() Ѕ»УЪБнТ»µг
Ѕ»УЪБнТ»µг![]() Ј®
Ј®
ўЩИфµг![]() ФЪЦ±ПЯ
ФЪЦ±ПЯ![]() ПВ·ЅЈ¬ЗТОЄЖЅТЖЗ°ЈЁ1Ј©ЦРµДЕЧОпПЯЙПµДµгЈ¬µ±ТФ
ПВ·ЅЈ¬ЗТОЄЖЅТЖЗ°ЈЁ1Ј©ЦРµДЕЧОпПЯЙПµДµгЈ¬µ±ТФ![]() Ўў
Ўў![]() Ўў
Ўў![]() ИэµгОЄ¶ҐµгµДИэЅЗРОКЗµИСьЦ±ЅЗИэЅЗРОК±Ј¬ЗуіцЛщУР·ыєПМхјюµДµг
ИэµгОЄ¶ҐµгµДИэЅЗРОКЗµИСьЦ±ЅЗИэЅЗРОК±Ј¬ЗуіцЛщУР·ыєПМхјюµДµг![]() µДЧш±кЈ»
µДЧш±кЈ»
ўЪИЎ![]() µДЦРµг
µДЦРµг![]() Ј¬Б¬ЅУ
Ј¬Б¬ЅУ![]() Ј¬
Ј¬![]() Ј¬Зу
Ј¬Зу![]() µДЧоґуЦµЈ®
µДЧоґуЦµЈ®
Ўѕґр°ёЎїЈЁ1Ј©![]() Ј»ЈЁ2Ј©ўЩ
Ј»ЈЁ2Ј©ўЩ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј»ўЪ
Ј»ўЪ![]() µДЧоґуЦµОЄ
µДЧоґуЦµОЄ![]() Ј®
Ј®
ЎѕЅвОцЎї
ЈЁ1Ј©ПИЗуіцµг![]() µДЧш±кЈ¬И»єуАыУГґэ¶ЁПµКэ·ЁЗуіцЕЧОпПЯµДєЇКэ±нґпКЅЈ»
µДЧш±кЈ¬И»єуАыУГґэ¶ЁПµКэ·ЁЗуіцЕЧОпПЯµДєЇКэ±нґпКЅЈ»
ЈЁ2Ј©ўЩКЧПИЗуіцЦ±ПЯ![]() µДЅвОцКЅєНПЯ¶О
µДЅвОцКЅєНПЯ¶О![]() µДі¤¶ИЈ¬ЧчОЄєуРшјЖЛгµД»щґЎЈ®
µДі¤¶ИЈ¬ЧчОЄєуРшјЖЛгµД»щґЎЈ®
Иф![]() ОЄµИСьЦ±ЅЗИэЅЗРОЈ¬ФтїЙ·ЦОЄТФПВБЅЦЦЗйїцЈє
ОЄµИСьЦ±ЅЗИэЅЗРОЈ¬ФтїЙ·ЦОЄТФПВБЅЦЦЗйїцЈє
µ±![]() ОЄЦ±ЅЗ±ЯК±Јєµг
ОЄЦ±ЅЗ±ЯК±Јєµг![]() µЅ
µЅ![]() µДѕаАлОЄ
µДѕаАлОЄ![]() Ј®ґЛК±Ј¬Ѕ«Ц±ПЯ
Ј®ґЛК±Ј¬Ѕ«Ц±ПЯ![]() ПтУТЖЅТЖ4ёцµҐО»єуЛщµГЦ±ПЯ
ПтУТЖЅТЖ4ёцµҐО»єуЛщµГЦ±ПЯ![]() УлЕЧОпПЯµДЅ»µгЈ¬јґОЄЛщЗуЦ®
УлЕЧОпПЯµДЅ»µгЈ¬јґОЄЛщЗуЦ®![]() µгЈ»
µгЈ»
µ±![]() ОЄР±±ЯК±Јєµг
ОЄР±±ЯК±Јєµг![]() µЅ
µЅ![]() µДѕаАлОЄ
µДѕаАлОЄ![]() Ј®ґЛК±Ј¬Ѕ«Ц±ПЯ
Ј®ґЛК±Ј¬Ѕ«Ц±ПЯ![]() ПтУТЖЅТЖ2ёцµҐО»єуЛщµГЦ±ПЯ
ПтУТЖЅТЖ2ёцµҐО»єуЛщµГЦ±ПЯ![]() УлЕЧОпПЯµДЅ»µгЈ¬јґОЄЛщЗуЦ®
УлЕЧОпПЯµДЅ»µгЈ¬јґОЄЛщЗуЦ®![]() µгЈ®
µгЈ®
ўЪУЙўЩїЙЦЄЈ¬![]() ОЄ¶ЁЦµЈ¬ТтґЛµ±
ОЄ¶ЁЦµЈ¬ТтґЛµ±![]() ИЎЧоРЎЦµК±Ј¬
ИЎЧоРЎЦµК±Ј¬![]() УРЧоґуЦµЈ®
УРЧоґуЦµЈ®
ИзґрНј2ЛщКѕЈ¬Ччµг![]() №ШУЪЦ±ПЯ
№ШУЪЦ±ПЯ![]() µД¶ФіЖµг
µД¶ФіЖµг![]() Ј¬УЙ·ЦОцїЙЦЄЈ¬µ±
Ј¬УЙ·ЦОцїЙЦЄЈ¬µ±![]() Ўў
Ўў![]() Ўў
Ўў![]() ЦРµгЈ©Иэµг№ІПЯК±Ј¬
ЦРµгЈ©Иэµг№ІПЯК±Ј¬![]() ЧоРЎЈ¬ЧоРЎЦµОЄПЯ¶О
ЧоРЎЈ¬ЧоРЎЦµОЄПЯ¶О![]() µДі¤¶ИЈ®
µДі¤¶ИЈ®
ЅвЈєЈЁ1Ј©![]() µИСьЦ±ЅЗИэЅЗРО
µИСьЦ±ЅЗИэЅЗРО![]() µД¶Ґµг
µД¶Ґµг![]() µДЧш±кОЄ
µДЧш±кОЄ![]() Ј¬
Ј¬![]() µДЧш±кОЄ
µДЧш±кОЄ![]()
![]() µг
µг![]() µДЧш±кОЄ
µДЧш±кОЄ![]() Ј®
Ј®
![]() ЕЧОпПЯ№э
ЕЧОпПЯ№э![]() Ј¬
Ј¬![]() БЅµгЈ¬
БЅµгЈ¬
![]()
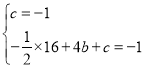 Ј¬
Ј¬
ЅвµГЈє![]() Ј¬
Ј¬![]() Ј¬
Ј¬
![]() ЕЧОпПЯµДєЇКэ±нґпКЅОЄЈє
ЕЧОпПЯµДєЇКэ±нґпКЅОЄЈє![]() Ј®
Ј®
ЈЁ2Ј©ўЩ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬
![]() Ц±ПЯ
Ц±ПЯ![]() µДЅвОцКЅОЄЈє
µДЅвОцКЅОЄЈє![]() Ј®
Ј®
ЙиЖЅТЖЗ°ЕЧОпПЯµД¶ҐµгОЄ![]() Ј¬ФтУЙЈЁ1Ј©їЙµГ
Ј¬ФтУЙЈЁ1Ј©їЙµГ![]() µДЧш±кОЄ
µДЧш±кОЄ![]() Ј¬ЗТ
Ј¬ЗТ![]() ФЪЦ±ПЯ
ФЪЦ±ПЯ![]() ЙПЈ®
ЙПЈ®
![]() µг
µг![]() ФЪЦ±ПЯ
ФЪЦ±ПЯ![]() ЙП»¬¶ЇЈ¬
ЙП»¬¶ЇЈ¬
![]() їЙЙи
їЙЙи![]() µДЧш±кОЄ
µДЧш±кОЄ![]() Ј¬
Ј¬
ФтЖЅТЖєуЕЧОпПЯµДєЇКэ±нґпКЅОЄЈє![]() Ј®
Ј®
Ѕв·ЅіМЧйЈє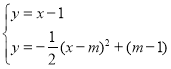 Ј¬
Ј¬
ЅвµГ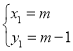 Ј¬
Ј¬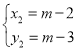
![]() Ј¬
Ј¬![]() Ј®
Ј®
№эµг![]() Чч
Чч![]() ЦбЈ¬№эµг
ЦбЈ¬№эµг![]() Чч
Чч![]() ЦбЈ¬Фт
ЦбЈ¬Фт
![]() Ј¬
Ј¬![]() Ј®
Ј®
![]() Ј®
Ј®
ИфТФ![]() Ўў
Ўў![]() Ўў
Ўў![]() ИэµгОЄ¶ҐµгµДµИСьЦ±ЅЗИэЅЗРОЈ¬ФтїЙ·ЦОЄТФПВБЅЦЦЗйїцЈє
ИэµгОЄ¶ҐµгµДµИСьЦ±ЅЗИэЅЗРОЈ¬ФтїЙ·ЦОЄТФПВБЅЦЦЗйїцЈє
µ±![]() ОЄЦ±ЅЗ±ЯК±Јєµг
ОЄЦ±ЅЗ±ЯК±Јєµг![]() µЅ
µЅ![]() µДѕаАлОЄ
µДѕаАлОЄ![]() ЈЁјґОЄ
ЈЁјґОЄ![]() µДі¤Ј©Ј®
µДі¤Ј©Ј®
УЙ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() їЙЦЄЈ¬
їЙЦЄЈ¬
![]() ОЄµИСьЦ±ЅЗИэЅЗРОЈ¬ЗТ
ОЄµИСьЦ±ЅЗИэЅЗРОЈ¬ЗТ![]() Ј¬
Ј¬![]() Ј®
Ј®
ИзНј1Ј¬№эµг![]() ЧчЦ±ПЯ
ЧчЦ±ПЯ![]() Ј¬Ѕ»ЕЧОпПЯ
Ј¬Ѕ»ЕЧОпПЯ![]() УЪµг
УЪµг![]() Ј¬Фт
Ј¬Фт![]() ОЄ·ыєПМхјюµДµгЈ®
ОЄ·ыєПМхјюµДµгЈ®
![]() їЙЙиЦ±ПЯ
їЙЙиЦ±ПЯ![]() µДЅвОцКЅОЄЈє
µДЅвОцКЅОЄЈє![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
ЅвµГ![]() Ј¬
Ј¬
![]() Ц±ПЯ
Ц±ПЯ![]() µДЅвОцКЅОЄЈє
µДЅвОцКЅОЄЈє![]() Ј®
Ј®
Ѕв·ЅіМЧй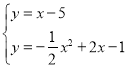 Ј¬
Ј¬
µГЈє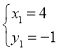 Ј¬
Ј¬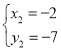
![]() Ј¬
Ј¬![]() Ј®
Ј®
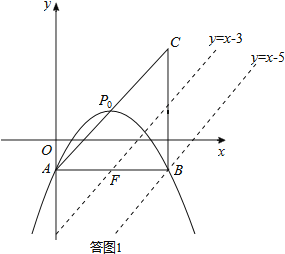
µ±![]() ОЄР±±ЯК±Јє
ОЄР±±ЯК±Јє![]() Ј¬їЙЗуµГµг
Ј¬їЙЗуµГµг![]() µЅ
µЅ![]() µДѕаАлОЄ
µДѕаАлОЄ![]() Ј®
Ј®
ИзґрНј2Ј¬ИЎ![]() µДЦРµг
µДЦРµг![]() Ј¬Фтµг
Ј¬Фтµг![]() µДЧш±кОЄ
µДЧш±кОЄ![]() Ј®
Ј®
УЙ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() їЙЦЄЈє
їЙЦЄЈє
![]() ОЄµИСьЦ±ЅЗИэЅЗРОЈ¬ЗТµг
ОЄµИСьЦ±ЅЗИэЅЗРОЈ¬ЗТµг![]() µЅЦ±ПЯ
µЅЦ±ПЯ![]() µДѕаАлОЄ
µДѕаАлОЄ![]() Ј®
Ј®
№эµг![]() ЧчЦ±ПЯ
ЧчЦ±ПЯ![]() Ј¬Ѕ»ЕЧОпПЯ
Ј¬Ѕ»ЕЧОпПЯ![]() УЪµг
УЪµг![]() Ј¬Фт
Ј¬Фт![]() ОЄ·ыєПМхјюµДµгЈ®
ОЄ·ыєПМхјюµДµгЈ®
![]() їЙЙиЦ±ПЯ
їЙЙиЦ±ПЯ![]() µДЅвОцКЅОЄЈє
µДЅвОцКЅОЄЈє![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
ЅвµГ![]() Ј¬
Ј¬
![]() Ц±ПЯ
Ц±ПЯ![]() µДЅвОцКЅОЄЈє
µДЅвОцКЅОЄЈє![]() Ј®
Ј®
Ѕв·ЅіМЧй Ј¬
Ј¬
µГЈє Ј¬
Ј¬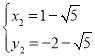
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј®
Ј®
ЧЫЙПЛщКцЈ¬ЛщУР·ыєПМхјюµДµг![]() µДЧш±кОЄЈє
µДЧш±кОЄЈє
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј®
Ј®
ўЪ![]() ґжФЪЧоґуЦµЈ®АнУЙИзПВЈє
ґжФЪЧоґуЦµЈ®АнУЙИзПВЈє
УЙўЩЦЄ![]() ОЄ¶ЁЦµЈ¬Фтµ±
ОЄ¶ЁЦµЈ¬Фтµ±![]() ИЎЧоРЎЦµК±Ј¬
ИЎЧоРЎЦµК±Ј¬![]() УРЧоґуЦµЈ®
УРЧоґуЦµЈ®
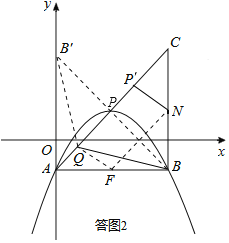
ИзґрНј2Ј¬ИЎµг![]() №ШУЪ
№ШУЪ![]() µД¶ФіЖµг
µД¶ФіЖµг![]() Ј¬ТЧµГµг
Ј¬ТЧµГµг![]() µДЧш±кОЄ
µДЧш±кОЄ![]() Ј¬
Ј¬![]() Ј®
Ј®
Б¬ЅУ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬
ТЧµГ![]() Ј¬ЗТ
Ј¬ЗТ![]() Ј¬
Ј¬
![]() ЛД±ЯРО
ЛД±ЯРО![]() ОЄЖЅРРЛД±ЯРОЈ®
ОЄЖЅРРЛД±ЯРОЈ®
![]() Ј®
Ј®
![]() Ј®
Ј®
![]() µ±
µ±![]() Ўў
Ўў![]() Ўў
Ўў![]() Иэµг№ІПЯК±Ј¬
Иэµг№ІПЯК±Ј¬![]() ЧоРЎЈ¬ЧоРЎЦµОЄ
ЧоРЎЈ¬ЧоРЎЦµОЄ![]() Ј®
Ј®
![]()
![]() µДЧоґуЦµОЄ
µДЧоґуЦµОЄ![]() Ј®
Ј®


 ФД¶БїміµПµБРґр°ё
ФД¶БїміµПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїМмГЕЙЅЛчµАКЗКАЅзЧоі¤µДёЯЙЅїНФЛЛчµАЈ¬О»УЪХЕјТЅзМмГЕЙЅѕ°ЗшЈ®ФЪТ»ґОјмРЮО¬»¤ЦРЈ¬јмРЮИЛФ±ґУЛчµАAґ¦їЄКјЈ¬СШA©ЃB©ЃCВ·ПЯ¶ФЛчµАЅшРРјмРЮО¬»¤Ј®ИзНјЈєТСЦЄ![]() ГЧЈ¬
ГЧЈ¬![]() ГЧЈ¬ABУлЛ®ЖЅПЯ
ГЧЈ¬ABУлЛ®ЖЅПЯ![]() µДјРЅЗКЗ
µДјРЅЗКЗ![]() Ј¬BCУлЛ®ЖЅПЯ
Ј¬BCУлЛ®ЖЅПЯ![]() µДјРЅЗКЗ
µДјРЅЗКЗ![]() Ј®ЗуЈє±ѕґОјмРЮЦРЈ¬јмРЮИЛФ±ЙПЙэµДґ№Ц±ёЯ¶И
Ј®ЗуЈє±ѕґОјмРЮЦРЈ¬јмРЮИЛФ±ЙПЙэµДґ№Ц±ёЯ¶И![]() КЗ¶аЙЩГЧЈї(Ѕб№ыѕ«И·µЅ1ГЧЈ¬ІОїјКэѕЭЈє
КЗ¶аЙЩГЧЈї(Ѕб№ыѕ«И·µЅ1ГЧЈ¬ІОїјКэѕЭЈє![]() )
)

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
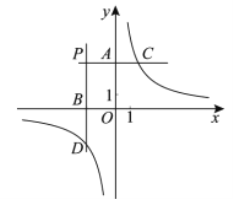
ЎѕМвДїЎїИзНјЈ¬·Ц±р№эµЪ¶юПуПЮДЪµДµг![]() Чч
Чч![]() Ј¬
Ј¬![]() ЦбµДЖЅРРПЯЈ¬Ул
ЦбµДЖЅРРПЯЈ¬Ул![]() Ј¬
Ј¬![]() Цб·Ц±рЅ»УЪµг
Цб·Ц±рЅ»УЪµг![]() Ј¬
Ј¬![]() Ј¬УлЛ«ЗъПЯ
Ј¬УлЛ«ЗъПЯ![]() ·Ц±рЅ»УЪµг
·Ц±рЅ»УЪµг![]() Ј¬
Ј¬![]() Ј®
Ј®
ПВГжИэёцЅбВЫЈ¬
ўЩґжФЪОЮКэёцµг![]() К№
К№![]() Ј»
Ј»
ўЪґжФЪОЮКэёцµг![]() К№
К№![]() Ј»
Ј»
ўЫґжФЪОЮКэёцµг![]() К№
К№![]() Ј®
Ј®
ЛщУРХэИ·ЅбВЫµДРтєЕКЗ__________Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
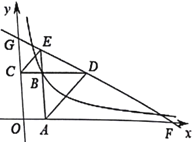
ЎѕМвДїЎїИзНјЈ¬ѕШРОOABCФЪЦ±ЅЗЧш±кПµЦРЈ¬СУі¤ABЦБµгEК№µГBE=BCБ¬ЅУCEЈ¬№эAЧчAD//CEЅ»CBСУі¤ПЯУЪµгDЈ¬Ц±ПЯDE·Ц±рЅ»xЦбЎўyЦбУЪFЎўGµгЈ¬ИфEGЈєDF=1Јє4Ј¬ЗТЎчBCEУлЎчBADГж»эЦ®єНОЄ![]() Ј¬Фт№эµг
Ј¬Фт№эµг![]() µДЛ«ЗъПЯ
µДЛ«ЗъПЯ![]() ЦР
ЦР![]() µДЦµОЄ____Ј®
µДЦµОЄ____Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
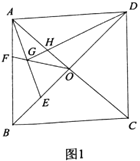
ЎѕМвДїЎїИзНјЈ¬Хэ·ЅРО![]() ЦРЈ®¶ФЅЗПЯACЎўBDЅ»УЪµг
ЦРЈ®¶ФЅЗПЯACЎўBDЅ»УЪµг![]() Ј®µг
Ј®µг![]() Ј¬µг
Ј¬µг![]() ·Ц±рФЪПЯ¶О
·Ц±рФЪПЯ¶О![]() Ј¬ПЯ¶О
Ј¬ПЯ¶О![]() ЙПЈ¬ЗТ
ЙПЈ¬ЗТ![]() Ј¬Б¬ЅУ
Ј¬Б¬ЅУ![]() Ѕ»
Ѕ»![]() УЪ
УЪ![]() Ј¬Б¬ЅУ
Ј¬Б¬ЅУ![]() Ѕ»
Ѕ»![]() УЪ
УЪ![]() Ј¬
Ј¬
ЈЁ1Ј©ИзНј1Ј¬Ифµг![]() ОЄПЯ¶О
ОЄПЯ¶О![]() ЦРµгЈ¬
ЦРµгЈ¬![]() Зу
Зу![]() µДі¤Ј»
µДі¤Ј»
ЈЁ2Ј©ИзНј2Ј¬Иф![]() ЖЅ·Ц
ЖЅ·Ц![]() Ј¬ЗуЦ¤Јє
Ј¬ЗуЦ¤Јє![]() Ј»
Ј»
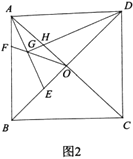
ЈЁ3Ј©ИзНј3Ј¬µг![]() ФЪПЯ¶О
ФЪПЯ¶О![]() (є¬¶Лµг)ЙПФЛ¶ЇЈ®Б¬ЅУ
(є¬¶Лµг)ЙПФЛ¶ЇЈ®Б¬ЅУ![]() Ј¬µ±ПЯ¶О
Ј¬µ±ПЯ¶О![]() і¤¶ИИЎµГЧоґуЦµК±Ј¬Ц±ЅУРґіц
і¤¶ИИЎµГЧоґуЦµК±Ј¬Ц±ЅУРґіц![]() µДЦµЈ®
µДЦµЈ®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНј1Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() КЗЦЈЦЭКР¶юЖЯЗшИэёцА¬»шґж·ЕµгЈ¬µг
КЗЦЈЦЭКР¶юЖЯЗшИэёцА¬»шґж·ЕµгЈ¬µг![]() Ј¬
Ј¬![]() ·Ц±рО»УЪµг
·Ц±рО»УЪµг![]() µДХэ±±єНХэ¶«·ЅПтЈ¬
µДХэ±±єНХэ¶«·ЅПтЈ¬![]() ГЧЈ®°ЛО»»·ОА№¤ИЛ·Ц±рІвµГµД
ГЧЈ®°ЛО»»·ОА№¤ИЛ·Ц±рІвµГµД![]() і¤¶ИИзПВ±нЈє
і¤¶ИИзПВ±нЈє
јЧ | ¶Ў | ±ы | ¶Ў | Ом | Рз | Йк | іЅ | |
| 84 | 76 | 78 | 82 | 70 | 84 | 86 | 80 |
ЛыГЗУЦµчІйБЛёчµгµДА¬»шБїЈ¬Іў»жЦЖБЛПВБРјдІ»НкХыµДНіјЖНј2Ј®
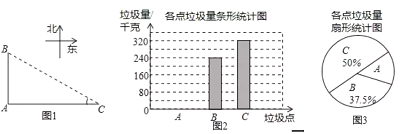
ЈЁ1Ј©±нЦРµДЦРО»КэКЗ ЎўЦЪКэКЗ Ј»
ЈЁ2Ј©Зу±нЦР![]() і¤¶ИµДЖЅѕщКэ
і¤¶ИµДЖЅѕщКэ![]() Ј»
Ј»
ЈЁ3Ј©Зу![]() ґ¦µДА¬»шБїЈ¬ІўЅ«Нј2І№ідНкХыЈ»
ґ¦µДА¬»шБїЈ¬ІўЅ«Нј2І№ідНкХыЈ»
ЈЁ4Ј©УГЈЁ2Ј©ЦРµД![]() ЧчОЄ
ЧчОЄ![]() µДі¤¶ИЈ¬ТЄЅ«
µДі¤¶ИЈ¬ТЄЅ«![]() ґ¦µДА¬»шСШµАВ·
ґ¦µДА¬»шСШµАВ·![]() ¶јФЛµЅ
¶јФЛµЅ![]() ґ¦Ј¬ТСЦЄФЛЛН1З§їЛА¬»шГїГЧµД·СУГОЄ0.005ФЄЈ¬ЗуФЛА¬»шЛщРиµД·СУГЈ®
ґ¦Ј¬ТСЦЄФЛЛН1З§їЛА¬»шГїГЧµД·СУГОЄ0.005ФЄЈ¬ЗуФЛА¬»шЛщРиµД·СУГЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
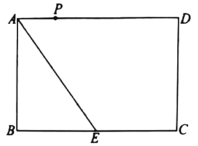
ЎѕМвДїЎїИзНјЈ¬ѕШРО![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() Ј¬EКЗ±Я
Ј¬EКЗ±Я![]() µДЦРµгЈ¬µгPФЪ±Я
µДЦРµгЈ¬µгPФЪ±Я![]() ЙПЈ¬Йи
ЙПЈ¬Йи![]() Ј¬ИфТФµгDОЄФІРДЈ¬
Ј¬ИфТФµгDОЄФІРДЈ¬![]() ОЄ°лѕ¶µД
ОЄ°лѕ¶µД![]() УлПЯ¶О
УлПЯ¶О![]() Ц»УРТ»ёц№«№ІµгЈ¬ФтЛщУРВъЧгМхјюµДxµДИЎЦµ·¶О§КЗ______Ј®
Ц»УРТ»ёц№«№ІµгЈ¬ФтЛщУРВъЧгМхјюµДxµДИЎЦµ·¶О§КЗ______Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДі№¤і§ЦЖЧч![]() БЅЦЦКЦ№¤ТХЖ·Ј¬
БЅЦЦКЦ№¤ТХЖ·Ј¬![]() ГїМмГїјю»сАы±И
ГїМмГїјю»сАы±И![]() ¶а105ФЄЈ¬»сАы30ФЄµД
¶а105ФЄЈ¬»сАы30ФЄµД![]() Ул»сАы240ФЄµД
Ул»сАы240ФЄµД![]() КэБїПаµИЈ®
КэБїПаµИЈ®
ЈЁ1Ј©ЦЖЧчТ»јю![]() єНТ»јю
єНТ»јю![]() ·Ц±р»сАы¶аЙЩФЄЈї
·Ц±р»сАы¶аЙЩФЄЈї
ЈЁ2Ј©№¤і§°ІЕЕ65ИЛЦЖЧч![]() Ј¬
Ј¬![]() БЅЦЦКЦ№¤ТХЖ·Ј¬ГїИЛГїМмЦЖЧч2јю
БЅЦЦКЦ№¤ТХЖ·Ј¬ГїИЛГїМмЦЖЧч2јю![]() »т1јю
»т1јю![]() Ј®ПЦФЪФЪІ»ФцјУ№¤ИЛµДЗйїцПВЈ¬ФцјУЦЖЧч
Ј®ПЦФЪФЪІ»ФцјУ№¤ИЛµДЗйїцПВЈ¬ФцјУЦЖЧч![]() Ј®ТСЦЄГїИЛГїМмїЙЦЖЧч1јю
Ј®ТСЦЄГїИЛГїМмїЙЦЖЧч1јю![]() ЈЁГїИЛГїМмЦ»ДЬЦЖЧчТ»ЦЦКЦ№¤ТХЖ·Ј©Ј¬ТЄЗуГїМмЦЖЧч
ЈЁГїИЛГїМмЦ»ДЬЦЖЧчТ»ЦЦКЦ№¤ТХЖ·Ј©Ј¬ТЄЗуГїМмЦЖЧч![]() Ј¬
Ј¬![]() БЅЦЦКЦ№¤ТХЖ·µДКэБїПаµИЈ®ЙиГїМм°ІЕЕ
БЅЦЦКЦ№¤ТХЖ·µДКэБїПаµИЈ®ЙиГїМм°ІЕЕ![]() ИЛЦЖЧч
ИЛЦЖЧч![]() Ј¬
Ј¬![]() ИЛЦЖЧч
ИЛЦЖЧч![]() Ј¬Рґіц
Ј¬Рґіц![]() Ул
Ул![]() Ц®јдµДєЇКэ№ШПµКЅЈ®
Ц®јдµДєЇКэ№ШПµКЅЈ®
ЈЁ3Ј©ФЪЈЁ1Ј©ЈЁ2Ј©µДМхјюПВЈ¬ГїМмЦЖЧч![]() І»ЙЩУЪ5јюЈ®µ±ГїМмЦЖЧч5јюК±Ј¬Гїјю»сАыІ»±дЈ®ИфГїФцјУ1јюЈ¬Фтµ±МмЖЅѕщГїјю»сАыјхЙЩ2ФЄЈ®ТСЦЄ
І»ЙЩУЪ5јюЈ®µ±ГїМмЦЖЧч5јюК±Ј¬Гїјю»сАыІ»±дЈ®ИфГїФцјУ1јюЈ¬Фтµ±МмЖЅѕщГїјю»сАыјхЙЩ2ФЄЈ®ТСЦЄ![]() Гїјю»сАы30ФЄЈ¬ЗуГїМмЦЖЧчИэЦЦКЦ№¤ТХЖ·їЙ»сµГµДЧЬАыИу
Гїјю»сАы30ФЄЈ¬ЗуГїМмЦЖЧчИэЦЦКЦ№¤ТХЖ·їЙ»сµГµДЧЬАыИу![]() ЈЁФЄЈ©µДЧоґуЦµј°ПаУ¦
ЈЁФЄЈ©µДЧоґуЦµј°ПаУ¦![]() µДЦµЈ®
µДЦµЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
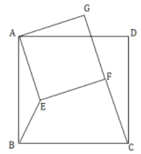
ЎѕМвДїЎїИзНјЈ¬ґуХэ·ЅРО![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬РЎХэ·ЅРО
Ј¬РЎХэ·ЅРО![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬ФЪРЎХэ·ЅРОИЖ
Ј¬ФЪРЎХэ·ЅРОИЖ![]() µгРэЧЄµД№эіМЦРЈ¬µ±
µгРэЧЄµД№эіМЦРЈ¬µ±![]() К±Ј¬ПЯ¶О
К±Ј¬ПЯ¶О![]() µДі¤ОЄ________Ј®
µДі¤ОЄ________Ј®
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com