
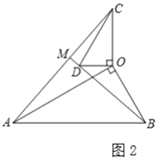
【题目】如图1,![]() ,
,![]() ,
,![]() 是郑州市二七区三个垃圾存放点,点
是郑州市二七区三个垃圾存放点,点![]() ,
,![]() 分别位于点
分别位于点![]() 的正北和正东方向,
的正北和正东方向,![]() 米.八位环卫工人分别测得的
米.八位环卫工人分别测得的![]() 长度如下表:
长度如下表:
甲 | 丁 | 丙 | 丁 | 戊 | 戌 | 申 | 辰 | |
| 84 | 76 | 78 | 82 | 70 | 84 | 86 | 80 |
他们又调查了各点的垃圾量,并绘制了下列间不完整的统计图2.
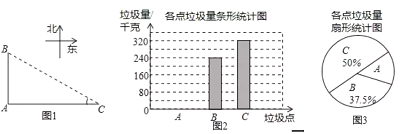
(1)表中的中位数是 、众数是 ;
(2)求表中![]() 长度的平均数
长度的平均数![]() ;
;
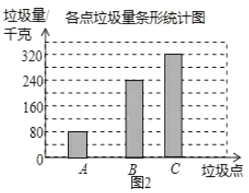
(3)求![]() 处的垃圾量,并将图2补充完整;
处的垃圾量,并将图2补充完整;
(4)用(2)中的![]() 作为
作为![]() 的长度,要将
的长度,要将![]() 处的垃圾沿道路
处的垃圾沿道路![]() 都运到
都运到![]() 处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.
处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.
【答案】(1)81米,84米;(2)80米;(3)80千克,图详见解析;(4)运垃圾所需的费用为![]() 元.
元.
【解析】
(1)根据中位数和众数的定义即可得;
(2)根据平均数的计算公式![]() 即可得;
即可得;
(3)先根据C处垃圾量的扇形统计图和条形统计图信息求出三处垃圾总量,再减去B、C两处的垃圾量可得A处的垃圾量,然后补全条形统计图即可;
(4)先利用勾股定理求出AB的长,再根据“运送1千克垃圾每米的费用为![]() 元”列出式子求解即可得.
元”列出式子求解即可得.
(1)由众数的定义得:众数是84米
由中位数的定义,先将表中的数据从小到大进行顺序为![]() ,则中位数是
,则中位数是![]() (米)
(米)
故答案为:81米,84米;
(2)由平均数的计算公式得:![]() (米)
(米)
答:表中![]() 长度的平均数
长度的平均数![]() 为80米;
为80米;
(3)A、B、C三处垃圾总量为![]() (千克)
(千克)
则![]() 处的垃圾总量是:
处的垃圾总量是:![]() (千克)
(千克)
补全条形统计图如下:
(4)在直角![]() 中,
中,![]() (米)
(米)
∵运送1千克垃圾每米的费用为![]() 元
元
∴运垃圾所需的费用为![]() (元)
(元)
答:运垃圾所需的费用为![]() 元.
元.


科目:初中数学 来源: 题型:
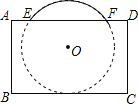
【题目】把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,点D是边BC上的动点,连接AD,点C关于直线AD的对称点为点E,射线BE与射线AD交于点F.


(1)在图1中,依题意补全图形;
(2)记![]() (
(![]() ),求
),求![]() 的大小;(用含
的大小;(用含![]() 的式子表示)
的式子表示)
(3)若△ACE是等边三角形,猜想EF和BC的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
对于任意正实数a、b,
∵![]() ,
,
![]()
![]() 当且仅当
当且仅当![]() 时,等号成立.
时,等号成立.
结论:在![]() 均为正实数)中,若
均为正实数)中,若![]() 为定值
为定值![]() 则
则![]() 当且仅当
当且仅当![]() 时,a+b有最小值
时,a+b有最小值![]() .
.
拓展:对于任意正实数![]() ,都有
,都有![]() 当且仅当
当且仅当![]() 时,等号成立.
时,等号成立.
在![]() (a、b、c均为正实数)中,若
(a、b、c均为正实数)中,若![]() 为定值
为定值![]() ,则
,则![]() 当且仅当
当且仅当![]() 时,
时,![]() 有最小值
有最小值![]()
例如:![]() 则
则![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
又如:若![]() 求
求![]() 的最小值时,因为
的最小值时,因为![]() 当且仅当
当且仅当![]() ,即
,即![]() 时等号成立,故当
时等号成立,故当![]() 时,
时,![]() 有最小值
有最小值![]() .
.
根据上述材料,解答下列问题:
(1)若a为正数,则当a=______时,代数式![]() 取得最小值,最小值为_____;
取得最小值,最小值为_____;
(2)已知函数![]() 与函数
与函数![]() ,求函数
,求函数![]() 的最小值及此时
的最小值及此时![]() 的值;
的值;
(3)我国某大型空载机的一次空载运输成本包含三部分:一是基本运输费用,共8100元;二是飞行耗油,每一百公里1200元;三是飞行报耗费用,飞行报耗费用与路程(单位:百公里)的平方成正比,比例系数为0.04,设该空载机的运输路程为![]() 百公里,则该空载机平均每一百公里的运输成本
百公里,则该空载机平均每一百公里的运输成本![]() 最低为多少?
最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线![]() (
(![]() 、
、![]() 为常数)的顶点为
为常数)的顶点为![]() ,等腰直角三角形
,等腰直角三角形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,
,![]() 的坐标为
的坐标为![]() ,直角顶点
,直角顶点![]() 在第四象限.
在第四象限.
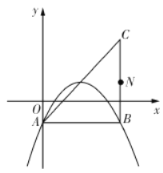
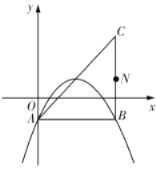
(1)如图,若该抛物线经过![]() 、
、![]() 两点,求该抛物线的函数表达式;
两点,求该抛物线的函数表达式;
(2)平移(1)中的抛物线,使顶点![]() 在直线
在直线![]() 上滑动,且与
上滑动,且与![]() 交于另一点
交于另一点![]() .
.
①若点![]() 在直线
在直线![]() 下方,且为平移前(1)中的抛物线上的点,当以
下方,且为平移前(1)中的抛物线上的点,当以![]() 、
、![]() 、
、![]() 三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点
三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点![]() 的坐标;
的坐标;
②取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
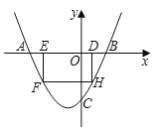
【题目】如图,抛物线![]() 与 x 轴交于点 A、B,与 y 轴交于点 C,且 OC=2OB, 点 D 为线段 OB 上一动点(不与点 B 重合),过点 D 作矩形 DEFH,点 H、F 在抛物线上,点 E 在 x 轴 上.
与 x 轴交于点 A、B,与 y 轴交于点 C,且 OC=2OB, 点 D 为线段 OB 上一动点(不与点 B 重合),过点 D 作矩形 DEFH,点 H、F 在抛物线上,点 E 在 x 轴 上.
(1)求抛物线的解析式;
(2)当矩形 DEFH 的周长最大时,求矩形 DEFH 的面积;
(3)在(2)的条件下,矩形 DEFH 不动,将抛物线沿着 x 轴向左平移 m 个单位,抛物线与矩形 DEFH的边交于点 M、N,连接 M、N.若 MN 恰好平分矩形 DEFH 的面积,求 m 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,∠BAD =90°,AC是对角线.点E在BC的延长线上,且∠CED =∠BAC.
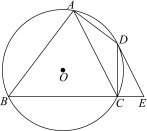
(1)判断DE与⊙O的位置关系,并说明理由;
(2)BA与CD的延长线交于点F,若DE∥AC,AB=4,AD =2,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+2ax-3与x轴交于A、B(1,0)两点(点A在点B的左侧),与y轴交于点C,将抛物线沿y轴平移m(m>0)个单位,当平移后的抛物线与线段OA有且只有一个交点时,则m的取值范围是_______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,在![]() 和
和![]() 中,
中,![]() ,连接
,连接![]() 交于点
交于点![]() .求证:
.求证:![]() ;并直接写出
;并直接写出![]() ______.
______.
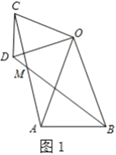
(2)类比探究:如图2,在![]() 和
和![]() 中,
中,![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() .请判断
.请判断![]() 的值及
的值及![]() 的度数.
的度数.
(3)拓展延伸:在(2)的条件下,将![]() 绕点
绕点![]() 在平面内旋转,
在平面内旋转,![]() 所在直线
所在直线![]() 交于点.若
交于点.若![]() ,请直接写出当点
,请直接写出当点![]() 与点
与点![]() 重合时
重合时![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com