
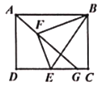
【题目】如图所示,已知矩形ABCD,AB=4,AD=3,点E为边DC上不与端点重合的一个动点,连接BE,将BCE沿BE翻折得到BEF,连接AF并延长交CD于点G,则线段CG的最大值是( )
A.1B.1.5C.4-![]() D.4-
D.4-![]()
【答案】D
【解析】
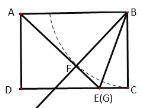
由图可知:DG最小时CG最大,故当∠GAD最小(∠GAB最大)时,CG取最大值,由F在以B为圆心,BC为半径的圆上得到AF⊥BF,此时点G、E重合,证明△ABF≌△AED,得到AE=AB=4,再利用勾股定理求出DE即可得到CG的最大值.
由图可知:DG最小时CG最大,故当∠GAD最小(∠GAB最大)时,CG取最大值,
∵F在以B为圆心,BC为半径的圆上,
∴AF与圆相切时,∠GAB最大,
即AF⊥BF,此时点G、E重合,
∵AB∥CD,
∴∠BAF=∠AED,
∵∠AFB=∠D=90°,BF=BC=AD,
∴△ABF≌△AED,
∴AE=AB=4,
∴DE=![]() ,
,
∴CE=CG=![]() ,
,
故选:D.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
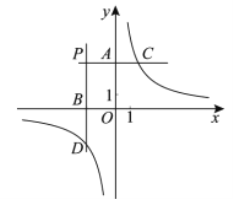
【题目】如图,分别过第二象限内的点![]() 作
作![]() ,
,![]() 轴的平行线,与
轴的平行线,与![]() ,
,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,与双曲线
,与双曲线![]() 分别交于点
分别交于点![]() ,
,![]() .
.
下面三个结论,
①存在无数个点![]() 使
使![]() ;
;
②存在无数个点![]() 使
使![]() ;
;
③存在无数个点![]() 使
使![]() .
.
所有正确结论的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂制作![]() 两种手工艺品,
两种手工艺品,![]() 每天每件获利比
每天每件获利比![]() 多105元,获利30元的
多105元,获利30元的![]() 与获利240元的
与获利240元的![]() 数量相等.
数量相等.
(1)制作一件![]() 和一件
和一件![]() 分别获利多少元?
分别获利多少元?
(2)工厂安排65人制作![]() ,
,![]() 两种手工艺品,每人每天制作2件
两种手工艺品,每人每天制作2件![]() 或1件
或1件![]() .现在在不增加工人的情况下,增加制作
.现在在不增加工人的情况下,增加制作![]() .已知每人每天可制作1件
.已知每人每天可制作1件![]() (每人每天只能制作一种手工艺品),要求每天制作
(每人每天只能制作一种手工艺品),要求每天制作![]() ,
,![]() 两种手工艺品的数量相等.设每天安排
两种手工艺品的数量相等.设每天安排![]() 人制作
人制作![]() ,
,![]() 人制作
人制作![]() ,写出
,写出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)在(1)(2)的条件下,每天制作![]() 不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知
不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知![]() 每件获利30元,求每天制作三种手工艺品可获得的总利润
每件获利30元,求每天制作三种手工艺品可获得的总利润![]() (元)的最大值及相应
(元)的最大值及相应![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小安填写的数学实践活动报告的部分内容
题 目 | 测量铁塔顶端到地面的高度 | |
测量目标示意图 |
|
|
相关数据 | CD=20m,ɑ=45°,β=52° | |
求铁塔的高度FE(结果精确到1米)(参考数据:sin52°≈0.79, cos52°≈0.62,tan52°≈1.28)
查看答案和解析>>
科目:初中数学 来源: 题型:
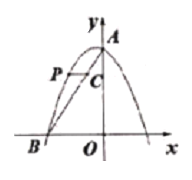
【题目】如图,二次函数y=-x2+(n-1)x+3的图像与y轴交于点A,与x轴的负半轴交于点B(-2,0)
(1)求二次函数的解析式;
(2)点P是这个二次函数图像在第二象限内的一线,过点P作y轴的垂线与线段AB交于点C,求线段PC长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】游泳池换水清洗的整个过程为“排水-清洗-注水”.一个长方体的游泳池在一次换水清洗的过程中,排水速度是注水速度的2倍,清洗的时间为![]() ,这次换水清洗过程中游泳池水量
,这次换水清洗过程中游泳池水量![]() 与时间
与时间![]() 之间的函数图像如图所示.
之间的函数图像如图所示.
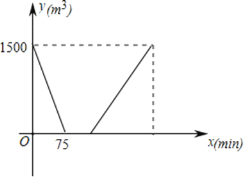
(1)这次换水清洗的过程中排水的速度为 ![]() .
.
(2)求“注水”过程中![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
(3)在该游泳池换水清洗的整个过程中,当池水的水位高度恰好是注满水的池中水位高度的![]() 时,直接写出
时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() 同时,点
同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() .过点
.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连
,连![]() 接,交
接,交![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() .解答下列问题:
.解答下列问题:
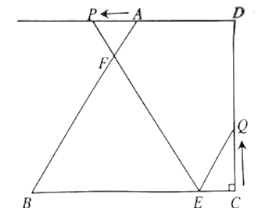
(1)当![]() 为何值时,
为何值时,![]() ?
?
(2)设五边形![]() 的面积为
的面积为![]() , 求
, 求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)连接![]() .是否存在某一时刻
.是否存在某一时刻![]() , 使点
, 使点![]() 在
在![]() 的垂直平分线上,若存在,求出的值;若不存在,说明理由.
的垂直平分线上,若存在,求出的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com