
【题目】函数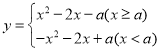 (
(![]() 为常数).
为常数).
(1)若点![]() 在函数图象上,求
在函数图象上,求![]() 的值;
的值;
(2)当![]() 时,若直线
时,若直线![]() (
(![]() 为常数)与函数恰好有三个交点时,设三个交点的横坐标从左至右依次为
为常数)与函数恰好有三个交点时,设三个交点的横坐标从左至右依次为![]() 、
、![]() 、
、![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)已知![]() 、
、![]() .若函数图象与线段
.若函数图象与线段![]() 有两个交点时,求
有两个交点时,求![]() 的取值范围;
的取值范围;
(4)当![]() 时,函数值
时,函数值![]() 满足
满足![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() 的值为-2或4;(2)
的值为-2或4;(2)![]() ;(3)
;(3)![]() 或
或![]() ;(4)
;(4)![]() 或
或![]() .
.
【解析】
(1)分![]() 和
和![]() 两种情况讨论,分别将
两种情况讨论,分别将![]() 代入对应的解析式求解即可;
代入对应的解析式求解即可;
(2)当![]() 时,若直线
时,若直线![]() (
(![]() 为常数)与函数恰好有三个交点,则
为常数)与函数恰好有三个交点,则![]() 与直线有2个交点,即可得到
与直线有2个交点,即可得到![]() ,且直线位于
,且直线位于![]() 顶点的下方,从而确定了m的取值,即可求得
顶点的下方,从而确定了m的取值,即可求得![]() ,从而得到结果;
,从而得到结果;
(3)分情况讨论,当![]() ,此时两段抛物线各有一个交点,若
,此时两段抛物线各有一个交点,若![]() ,此时
,此时![]() 需与AB有2个交点,据此进行计算即可;
需与AB有2个交点,据此进行计算即可;
(4)分别讨论![]() 和
和![]() 两种情况,分别计算出当
两种情况,分别计算出当![]() ,
,![]() 时y的取值,然后计算判断范围即可.
时y的取值,然后计算判断范围即可.
解:(1)若![]() ,则将
,则将![]() 代入
代入![]() ,
,
![]() ,解得
,解得![]() ,成立,
,成立,
若![]() ,则将
,则将![]() 代入
代入![]() ,
,
![]() ,解得
,解得![]() ,成立,
,成立,
故![]() 的值为-2或4;
的值为-2或4;
(2)当![]() 时,
时,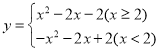 ,
,
![]() 的对称轴为
的对称轴为![]() ,
,
∵![]() ,∴该图象仅有右半支的一部分,
,∴该图象仅有右半支的一部分,
![]() 时
时![]() ,
,
![]() 的对称轴为
的对称轴为![]() ,
,
∵![]() ,∴该图象对称轴两侧均有图象,
,∴该图象对称轴两侧均有图象,
![]() 时
时![]() ,
,
![]() 时
时![]() ,
,
在![]() 上,令
上,令![]() ,解得
,解得![]() (舍),
(舍),![]() ,
,
若直线![]() (
(![]() 为常数)与函数恰好有三个交点时,
为常数)与函数恰好有三个交点时,
则![]() ,
,
∴![]() ,即
,即![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)若![]() ,此时两段抛物线各有一个交点,
,此时两段抛物线各有一个交点,
将![]() 代入
代入![]() ,
,
解得![]() ,
,
若![]() 与AB有交点则
与AB有交点则![]()
在![]() ,上,
,上,
若![]() 时,y=2,则
时,y=2,则![]() ,
,
解得![]() 或
或![]() ,
,
若![]() 与AB有交点则
与AB有交点则![]() ,
,
∴![]() ;
;
若![]() ,此时
,此时![]() 需与AB有2个交点,
需与AB有2个交点,
将![]() 代入
代入![]() ,
,
解得![]() ,
,
由对称轴为直线![]() ,可知,若
,可知,若![]() 需与AB有2个交点,
需与AB有2个交点,
则当y=2时,![]() ,
,
整理为![]() ,
,
则![]() ,解得
,解得![]() ,
,
∴![]() ,
,
综上所述,![]() 或
或![]() ;
;
(4)当![]() 时,
时,![]() 在
在![]() 范围,
范围,
x=1,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
解得![]() (舍)或
(舍)或![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
解得![]() ,
,
∴![]() ,
,
当![]() 时,
时,
x=-1,![]() ,满足范围,
,满足范围,
因此x=2a,和x=2a+1时,![]() ,
,
在![]() 中,
中,
![]() ,
,![]() ,
,![]() ,
,
解得![]() ,
,
![]() ,
,![]() ,
,![]() ,恒成立,
,恒成立,
∵![]()
∴![]()
综上所述![]() 或
或![]() .
.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
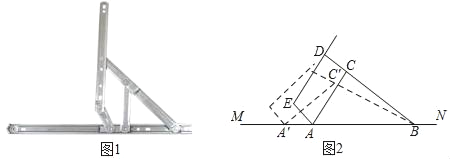
【题目】“滑块铰链”是一种用于连接窗扇和窗框,使窗户能够开启和关闭的连杆式活动链接装置(如图1).图2是“滑块铰链”的平面示意图,滑轨MN安装在窗框上,悬臂DE安装在窗扇上,支点B、C、D始终在一条直线上,已知托臂AC=20厘米,托臂BD=40厘米,支点C,D之间的距离是10厘米,张角∠CAB=60°.
(1)求支点D到滑轨MN的距离(精确到1厘米);
(2)将滑块A向左侧移动到A′,(在移动过程中,托臂长度不变,即AC=A′C′,BC=BC′)当张角∠C′A'B=45°时,求滑块A向左侧移动的距离(精确到1厘米).(备用数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45,
≈2.45,![]() ≈2.65)
≈2.65)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:P(1,0)、Q(2,﹣2)都是“整点”.抛物线y=mx2﹣4mx+4m﹣2(m>0)与x轴交于点A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是( )
A. ![]() ≤m<1B.
≤m<1B. ![]() <m≤1C. 1<m≤2D. 1<m<2
<m≤1C. 1<m≤2D. 1<m<2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() 长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
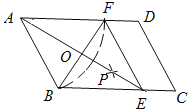
(1)四边形ABEF是_______;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为________,∠ABC=________°.(直接填写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1,B1D1相交于点O.以点O为坐标原点,分别以OA1,OB1所在直线为x轴、y轴,建立如图所示的直角坐标系.以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,在x轴的正半轴上得到点A1,A2,A3,…,An,则点An的坐标为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com