
【题目】如图,已知双曲线y= ![]() 经过点B(3
经过点B(3 ![]() ,1),点A是双曲线第三象限上的动点,过B作BC⊥y轴,垂足为C,连接AC.
,1),点A是双曲线第三象限上的动点,过B作BC⊥y轴,垂足为C,连接AC. 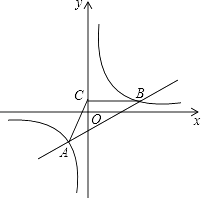
(1)求k的值;
(2)若△ABC的面积为6 ![]() ,求直线AB的解析式;
,求直线AB的解析式;
(3)在(2)的条件下,写出反比例函数值大于一次函数值时x的取值范围.
【答案】
(1)解:把B(3 ![]() ,1)代入y=
,1)代入y= ![]() 中得,1=
中得,1= ![]() ,
,
∴k=3 ![]()
(2)解:设△ABC中BC边上的高为h,
∵BC⊥y轴,B(3 ![]() ,1)
,1)
∴BC=3 ![]() ,
,
∵△ABC的面积为6 ![]() ,
,
∴ ![]() BCh=6
BCh=6 ![]() ,
,
∴h=4,
∴点A的纵坐标为1﹣4=﹣3,
把y=﹣3代入y= ![]() ,
,
∴x=﹣ ![]() ,
,
∴A(﹣ ![]() ,﹣3),设直线AB的解析式为:y=mx+n,
,﹣3),设直线AB的解析式为:y=mx+n,
把A(﹣ ![]() ,﹣3)和B(3
,﹣3)和B(3 ![]() ,1)代入y=mx+n,
,1)代入y=mx+n,
![]() 解得:
解得: 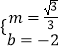
∴直线AB的解析式为y= ![]() ﹣2
﹣2
(3)解:由图象可得:x<﹣ ![]() 或0<x<3
或0<x<3 ![]()
【解析】(1)将B的坐标代入双曲线的解析式即可求出k的值.(2)设△ABC中BC边上的高为h,由△ABC的面积为6 ![]() 可求出h的值,从而可求出A的纵坐标为﹣3,然后即可求出点A的坐标,最后将A与B的坐标代入一次函数的解析式即可求出答案.(3)找出反比例函数图象位于一次函数图象上方的部分即可求出x的范围.
可求出h的值,从而可求出A的纵坐标为﹣3,然后即可求出点A的坐标,最后将A与B的坐标代入一次函数的解析式即可求出答案.(3)找出反比例函数图象位于一次函数图象上方的部分即可求出x的范围.


科目:初中数学 来源: 题型:
【题目】如图,I点为△ABC的内心,D点在BC上,且ID⊥BC,若∠B=44°,∠C=56°,则∠AID的度数为何?( )

A. 174 B. 176 C. 178 D. 180
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在篮球比赛中,某队员连续10场比赛中每场的得分情况如下所示:
场次(场) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
得分(分) | 13 | 4 | 13 | 16 | 6 | 19 | 4 | 4 | 7 | 18 |
则这10场比赛中该队员得分的中位数和众数分别是( )
A.10,4
B.10,13
C.11,4
D.12.5,13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为半圆上一动点,过点C作⊙O的切线l的垂线BD,垂足为D,BD与⊙O交于点E,连接OC,CE,AE,AE交OC于点F. 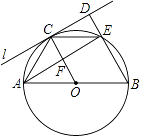
(1)求证:△CDE≌△EFC;
(2)若AB=4,连接AC. ①当AC=时,四边形OBEC为菱形;
②当AC=时,四边形EDCF为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+2经过A(﹣1,0),B(2,0),C三点.直线y=mx+ ![]() 交抛物线于A,Q两点,点P是抛物线上直线AQ上方的一个动点,作PF⊥x轴,垂足为F,交AQ于点N.
交抛物线于A,Q两点,点P是抛物线上直线AQ上方的一个动点,作PF⊥x轴,垂足为F,交AQ于点N.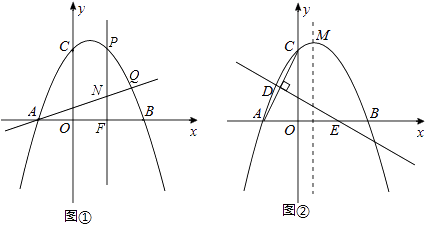
(1)求抛物线的解析式;
(2)如图①,当点P运动到什么位置时,线段PN=2NF,求出此时点P的坐标;
(3)如图②,线段AC的垂直平分线交x轴于点E,垂足为D,点M为抛物线的顶点,在直线DE上是否存在一点G,使△CMG的周长最小?若存在,请求出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
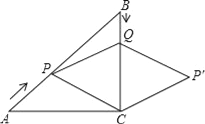
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒![]() cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,若四边形QPCP′为菱形,则t的值为_____.
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,若四边形QPCP′为菱形,则t的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是由几个相同的小正方体搭成的几何体,
(1)搭成这个几何体需要 个小正方体;
(2)画出这个几何体的主视图和左视图;
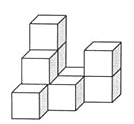
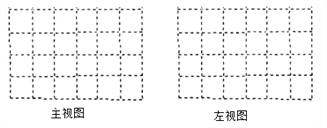
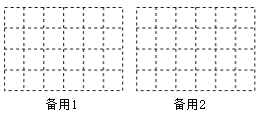
(3)在保持主视图和左视图不变的情况下,最多可以拿掉n个小正方体,则n= ,请在备用图中画出拿掉n个小正方体后新的几何体的俯视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知∠B和∠C的平分线相交于点F,经过点F作DE//BC,交AB于D,交AC于点E,若BD+CE=9,则线段DE的长为( )
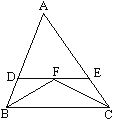
A. 9 B. 8 C. 7 D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com