
【题目】如图,等腰![]() 中,
中,![]() ,
,![]() .动点
.动点![]() 在
在![]() 上以每分钟5个单位长度的速度从
上以每分钟5个单位长度的速度从![]() 点出发向
点出发向![]() 点移动,过
点移动,过![]() 作
作![]() 交
交![]() 边于
边于![]() 点,连结
点,连结![]() 、
、![]() .设
.设![]() 点移动的时间为
点移动的时间为![]() .
.
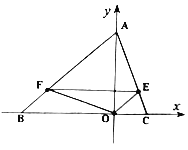
(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)计算:当![]() 面积最大时,
面积最大时,![]() 的值;
的值;
(3)在(2)的条件下,边![]() 上是否还存在一个点
上是否还存在一个点![]() ,使得
,使得![]() ?若存在,请直接写出
?若存在,请直接写出![]() 点的坐标;若不存在,试说明理由.
点的坐标;若不存在,试说明理由.
【答案】(1)A(0,6),B(-8,0);(2)当t=1时,△EFO的面积达到最大值;(3)存在满足条件的D点,其坐标为(-3,0)
【解析】
(1)先根据题意得出AC两点的坐标,再设BO=x,由勾股定理求出x的值,进而可得出B点坐标;
(2)过F点作FK⊥BC于K,设F点移动的时间为t,证明△AFE∽△ABC,利用相似的性质得出EF=10-5t,从而得到S△EFO=-![]() (t-2)t,从而得出结果;
(t-2)t,从而得出结果;
(3)在(2)的条件下,E、F分别是AC、AB的中点,若使D为BC的中点时,![]() ,再由
,再由![]() 可知FO=ED,EO=FD,EF=FE,故△EFD≌△FEO,从而可得出D点坐标.
可知FO=ED,EO=FD,EF=FE,故△EFD≌△FEO,从而可得出D点坐标.
解:(1)∵CO=2,
∴C(2,0),
又∵AO=3OC=6,
∴A(0,6),
可设BO=x,且x>0,
则:BC2=(2+x)2,AB2=AO2+OB2=36+x2,
又∵BC=AB,
∴(2+x)2=36+x2,
解得:x=8,
∴B(-8,0);
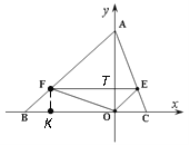
(2)过F点作FK⊥BC于K,
可设F点移动的时间为t,且0<t<2,
则:BF=5t,TO=FK=3t;
∴AT=6-3t,
又∵FE∥BC,
∴△AFE∽△ABC,
而AO⊥BC交EF于T,
则:![]() =
=![]() ,
,
∴![]() =
=![]() ,即:EF=10-5t,
,即:EF=10-5t,
故:S△EFO=![]() EF×TO=
EF×TO=![]() (10-5t)×3t,
(10-5t)×3t,
即:S△EFO=-![]() (t-2)t,
(t-2)t,
∴当t=1时,△EFO的面积达到最大值;
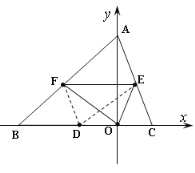
(3)在(2)的基础上,E、F分别是AC、AB的中点,
若使D为BC的中点时,
![]() ,
,
又∵![]() ,
,
∴FO=ED,EO=FD,EF=FE,
在△EFD和△FEO中,
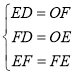 ,
,
则△EFD≌△FEO(SSS),
∵B(-8,0),C(2,0),
∴D(-3,0),
故:存在满足条件的D点,其坐标为(-3,0).


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
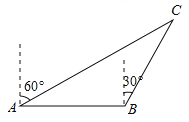
【题目】如图,海中有一灯塔C,它的周围11海里内有暗礁.一渔船以18海里/时的速度由西向东航行,在A点测得灯塔C位于北偏东60°的方向上,航行40分钟到达B点,此时测得灯塔C位于北偏东30°的方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交x轴于点A(-3,0)和点B,交y轴于点C(0,3).
交x轴于点A(-3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
(3)点G是抛物线上的动点,点F在x轴上的动点,若以A,C,F,G四个点为顶点的四边形是平行四边形,求出所有满足条件的点F坐标(直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数给出如下定义:对于函数![]() ,若当
,若当![]() ,函数值
,函数值![]() 满足
满足![]() ,且满足
,且满足![]() ,则称此函数为“
,则称此函数为“![]() 属和合函数”.
属和合函数”.
例如:正比例函数![]() ,当
,当![]() 时,
时,![]() ,则
,则![]() ,求得:
,求得:![]() ,所以函数
,所以函数![]() 为“3属和合函数”.
为“3属和合函数”.
(1)若一次函数![]() 为“1属和合函数”,则
为“1属和合函数”,则![]() 的值_________;
的值_________;
(2)已知二次函数![]() ,当
,当![]() 时,
时,![]() 是“
是“![]() 属和合函数”,则
属和合函数”,则![]() 的取值范围_________.
的取值范围_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“江山如此多娇”为主题的地理知识竞赛活动,要求每班派出一名同学代表本班参赛.九年一班四名同学主动报名,老师为了确定最终参赛人选,对这四名同学的历次地理考试成绩进行了汇总,数据如下:

班级里数学小组的同学对上面的数据进行了进一步的整理:

根据以上的信息,回答下列问题:
(1)写出上表中![]() ,
,![]() ,
,![]() .
.
(2)丙同学看到统计表,对老师说:“我的成绩方差最小,说明我的成绩最稳定,应该派我去参赛!”请问你是否同意他的观点?若你是老师,你将派谁参赛?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,E,F分别为AD,AB上的点,且AE=AF,连接EF并延长,交CB的延长线于点G,连接BD.
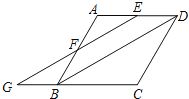
(1) 求证:四边形EGBD是平行四边形;
(2) 连接AG,若∠FGB=![]() ,GB=AE=3,求AG的长.
,GB=AE=3,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() 是
是![]() 的中点,直线
的中点,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)如图,若点![]() 在线段
在线段![]() 上,线段
上,线段![]() 和
和![]() 之间的数量关系是 ,位置关系是 ;
之间的数量关系是 ,位置关系是 ;
(2)在(1)的条件下,当点![]() 在线段
在线段![]() 上,且
上,且![]() 时,求证:
时,求证:![]() ;
;
(3)当点![]() 在线段
在线段![]() 的延长线上时,在线段
的延长线上时,在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
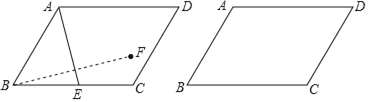
【题目】如图,已知ABCD中,∠ABC=60°,AB=4,BC=m,E为BC边上的动点,连结AE,作点B关于直线AE的对称点F.
(1)若m=6,①当点F恰好落在∠BCD的平分线上时,求BE的长;
②当E、C重合时,求点F到直线BC的距离;
(2)当点F到直线BC的距离d满足条件:2![]() ﹣2≤d≤2
﹣2≤d≤2![]() +4,求m的取值范围.
+4,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com