
【题目】如图,在等边△ABC中,点D,E分别在边BC,AC上,且AE=CD,BE与AD相交于点P,BQ上AD于点Q.

(1)求证:AD=BE;
(2)求∠PBQ的度数;
(3)若PQ=3,PE=1,求AD的长.
【答案】(1)证明详见解析;(2)∠PBQ=30°;(3)AD=7.
【解析】
(1)根据等边三角形的性质,通过全等三角形的判定定理SAS证得△AEB≌△CDA,根据全等三角形的性质即可得到结论;
(2)利用(1)中的全等三角形的对应角相等和三角形外角的性质求得∠BPQ=60°,再由直角三角形两锐角互余即可得到结论;
(3)由“30度角所对的直角边是斜边的一半”得到2PQ=BP=6,则易求BE=BP+PE=7.
(1)∵△ABC为等边三角形,∴AB=CA,∠BAE=∠C=60°.
在△AEB与△CDA中,∵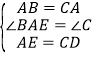 ,∴△AEB≌△CDA(SAS),∴AD=BE;
,∴△AEB≌△CDA(SAS),∴AD=BE;
(2)由(1)知,△AEB≌△CDA,则∠ABE=∠CAD,∴∠BAD+∠ABE=∠BAD+∠CAD=∠BAC=60°,∴∠BPQ=∠BAD+∠ABE=60°.
在Rt△PBQ中,∠PBQ=90°-∠BPQ=90°-60°=30°;
(3)∵∠PBQ=30°,∴PQ=![]() BP=3,∴BP=6,∴BE=BP+PE=7,即AD=7.
BP=3,∴BP=6,∴BE=BP+PE=7,即AD=7.
故答案为:7.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,某电信部门计划修建一条连接B、C两地的电缆.测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200m,电缆BC至少长多少米(精确到1m)?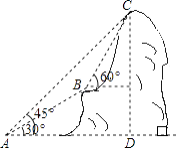
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数 ![]() 的图象如图所示,则结论: ①两函数图象的交点A的坐标为(2,2);
的图象如图所示,则结论: ①两函数图象的交点A的坐标为(2,2);
②当x>2时,y2>y1;
③当x=1时,BC=3;
④当x逐渐增大时,y1随着x的增大而增大,y2随着x的增大而减小.
其中正确结论的序号是 . 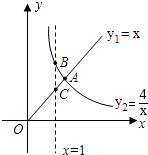
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系中,点A、B、C的坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).
(1)作△ABC关于y对称的△A1B1C1,其中,点A、B、C的对应点分别为A1、B1、C1(不要求写作法);
(2)写出点A1、B1、C1的坐标;
(3)计算△A1B1C1的面积.
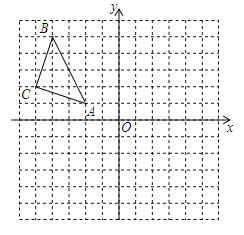
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分类讨论,在平面直角坐标系中,已知A(2,3),B(0,2),C(3,0).将三角形ABC的一个顶点平移到坐标原点O处,写出平移方法和另两个对应顶点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地决策,自来水公司随机抽取部分用户的用适量数据,并绘制了如下不完整统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:

(1)此次调查抽取了多少用户的用水量数据?
(2)补全频数分布直方图,求扇形统计图中“25吨~30吨”部分的圆心角度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地20万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD为△ABC的高线,AD=BC,以AB为底边作等腰Rt△ABE,连接ED,EC,延长CE交AD于F点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有( )

A. ①③ B. ①②④ C. ①②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)-a2b+(3ab2-a2b)-2(2ab2-a2b),其中a=1,b=-2;
(2)-6x+3(3x2-1)-(9x2-x+3),其中x=-![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com