练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】动手操作：（不要求写作法和证明，只保留作图痕迹）

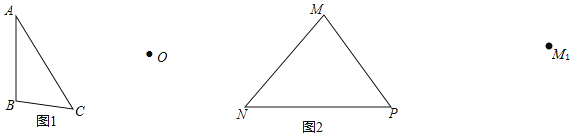
    （1）如图所示，以点为对称中心，画出与成中心对称的图形．

    （2）如图所示，将绕点旋转后，顶点旋转到了处，试画出旋转后的．

    【答案】（1）如图所示，即为所求；见解析；（2）如图所示，即为所求；见解析．

    【解析】

    （1）依据中心对称的性质，分别连接AO并延长使A1O=AO，连接BO并延长使B1O=BO，连接CO并延长使C1O=CO，即可得到与△ABC成中心对称的图形△A1B1C1；
    （2）依据旋转的方向，旋转角度以及旋转中心，连接PM1，作∠NPN1=∠MPM1，再在射线PN1上截取PN=PN1即可得到旋转后的△M1N1P．

    解：（1）如图所示，△A1B1C1即为所求：

    （2）如图所示，△M1N1P即为所求：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

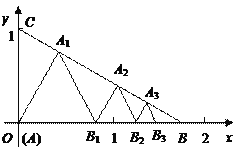
    【题目】如图所示，已知：点A(0，0)，B（，0），C（0，1）在△ABC内依次作等边三角形，使一边在x轴上，另一个顶点在BC边上，作出的等边三角形分别是第1个△AA1B1，第2个△B1A2B2，第3个△B2A3B3，…，则第个等边三角形的边长等于__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们给出如下定义：有一组相邻内角相等的四边形叫做等邻角四边形．请解答下列问题：

    （1）写出一个你所学过的特殊四边形中是等邻角四边形的图形的名称；

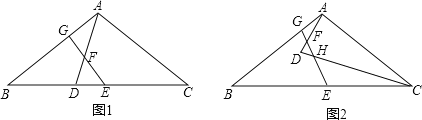
    （2）如图1，在△ABC中，AB＝AC，点D在BC上，且CD＝CA，点E、F分别为BC、AD的中点，连接EF并延长交AB于点G．求证：四边形AGEC是等邻角四边形；

    （3）如图2，若点D在△ABC的内部，（2）中的其他条件不变，EF与CD交于点H，图中是否存在等邻角四边形，若存在，指出是哪个四边形，并证明；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，某学校有一边长为20米的正方形区域（四周阴影是四个全等的矩形，记为区域甲；中心区是正方形，记为区域乙）．区域甲建设成休闲区，区域乙建成展示区，已知甲、乙两个区域的建设费用如下表：

    区域

    甲

    乙

    价格（百元米2）

    6

    5

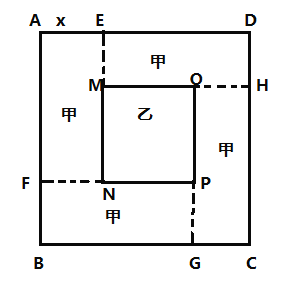
    设矩形的较短边的长为米，正方形区域建设总费用为百元．

    （1）的长为 米（用含的代数式表示）；

    （2）求关于的函数解析式；

    （3）当中心区的边长要求不低于8米且不超过12米时，预备建设资金220000元够用吗？请利用函数的增减性来说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某小组做“用频率估计概率”的实验时，绘出的某一结果出现的频率折线图，则符合这一结果的实验可能是（　　）

    A. 抛一枚硬币，出现正面朝上

    B. 掷一个正六面体的骰子，出现3点朝上

    C. 一副去掉大小王的扑克牌洗匀后，从中任抽一张牌的花色是红桃

    D. 从一个装有2个红球1个黑球的袋子中任取一球，取到的是黑球

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，P是等边三角形ABC内的一点，且PA=3，PB=4，PC=5，将△ABP绕点B顺时针旋转60°到△CBQ位置．连接PQ，则以下结论错误的是（　　）

    A. ∠QPB=60° B. ∠PQC=90° C. ∠APB=150° D. ∠APC=135°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一元二次方程x2+2x﹣3＝0的二根x1，x2（x1＜x2）是抛物线y＝ax2+bx+c与x轴的两个交点B，C的横坐标，且此抛物线过点A（3，6）．

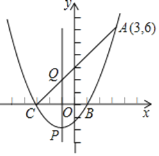
    （1）求此二次函数的解析式；

    （2）写出不等式ax2+bx+c≥0的解集；

    （3）设此抛物线的顶点为P，对称轴与线段AC相交于点Q，求点P和点Q的坐标；

    （4）在x轴上有一动点M，当MQ+MA取得最小值时，求M点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某企业设计了一款工艺品，每件成本40元，出于营销考虑，要求每件售价不得低于40元，但物价部门要求每件售价不得高于60元．据市场调查，销售单价是50元时，每天的销售量是100件，而销售单价每涨1元，每天就少售出2件，设单价上涨元．

    （1）求当为多少时每天的利润是1350元？

    （2）设每天的销售利润为，求销售单价为多少元时，每天利润最大？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y＝﹣x2+2x+8与x轴交于B、C两点，点D平分BC，且点A为抛物线上的点，且∠BAC为锐角，则AD的值范围为_____．

    查看答案和解析>>

    同步练习册答案