
����Ŀ����ͼ���ڳ���Ϊ1����λ���ȵ�С��������ɵ������������У���ABC����������A��B��C���ڸ����.
��1����ͼ1�л�������ABC����ֱ��l����ԳƵ���A1B1C1��
��2����ͼ1��ֱ��l���ҳ�һ��Q,ʹ�� QA+QC1��ֵ��С��
��3����ͼ1��ֱ��l���ҳ�һ��P,ʹ�� |PAPC1| ��ֵ���
��4����ͼ2�У���һ��![]() ��E��F���ڸ���ϣ�ʹ�߶�BCΪ��BEF�Ľ�ƽ����
��E��F���ڸ���ϣ�ʹ�߶�BCΪ��BEF�Ľ�ƽ����

 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
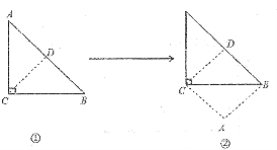
����Ŀ����֪����ͼ����ABC�У���A��90����AB��AC��D��BC���ϵ��е㣬E��F�ֱ���AB��AC�ϵĵ㣬�ҡ�EDF��90������֤��BE��AF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ա߳�Ϊ2�������ε�����OΪ�˵㣬���������ֱ�����ߣ��ֱ��������εı߽���A��B���㣬���߶�AB����Сֵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�AΪy����������һ�㣬����A��x���ƽ���ߣ�������![]() ��ͼ����B�㣬������
��ͼ����B�㣬������![]() ��ͼ����C����C��y���ƽ���߽�BO���ӳ�����D��
��ͼ����C����C��y���ƽ���߽�BO���ӳ�����D��
��1�������A������Ϊ��0��2�������߶�AB���߶�CA�ij���֮�ȣ�
��2�������A������Ϊ��0��a�������߶�AB���߶�CA�ij���֮�ȣ�
��3���ڣ�1�������£��ı���AODC�����Ϊ���٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ���⣺����![]() ������m��n��������������m��2��n��1����
������m��n��������������m��2��n��1����
̽�����⣺Ϊ����������ѧ���⣬�����������ν�ϵ�˼�뷽����ͨ�����ϵطָ�һ�����Ϊ1�������Σ���������ϵ�ͼ���ͼ������ؽ������������ȡһ���������⻯�IJ���������̽����
̽��һ������![]() ��
��
��1�ηָ�������ε�������ȷ֣�������Ӱ���ֵ����Ϊ![]() ��
��
��2�ηָ���ϴηָ�ͼ�пհײ��ֵ�����������ȷ֣���Ӱ���ֵ����֮��Ϊ![]() +
+![]() ��
��
��3�ηָ���ϴηָ�ͼ�пհײ��ֵ�����������ȷ֣�����
��
��n�ηָ���ϴηָ�ͼ�пհײ��ֵ���������ȷ֣�������Ӱ���ֵ����֮��Ϊ![]() +
+![]() +
+![]() +��+
+��+![]() �����հײ��ֵ������
�����հײ��ֵ������![]() ��
��
���ݵ�n�ηָ�ͼ�ɵõ�ʽ��![]() +
+![]() +
+![]() +��+
+��+![]() =1��
=1��![]() ��
��

̽����������![]() +
+![]() +
+![]() +��+
+��+![]() ��
��
��1�ηָ�������ε�������ȷ֣�������Ӱ���ֵ����Ϊ![]() ��
��
��2�ηָ���ϴηָ�ͼ�пհײ��ֵ�����������ȷ֣���Ӱ���ֵ����֮��Ϊ![]() +
+![]() ��
��
��3�ηָ���ϴηָ�ͼ�пհײ��ֵ�����������ȷ֣�����
��
��n�ηָ���ϴηָ�ͼ�пհײ��ֵ����������ȷ֣�������Ӱ���ֵ����֮��Ϊ![]() +
+![]() +
+![]() +��+
+��+![]() �����հײ��ֵ������
�����հײ��ֵ������![]() ��
��
���ݵ�n�ηָ�ͼ�ɵõ�ʽ��![]() +
+![]() +
+![]() +��+
+��+![]() =1��
=1��![]() ��
��
����ͬ����2����![]() +
+![]() +
+![]() +��+
+��+![]() =
=![]() ��
��![]() ��
��

̽����������![]() +
+![]() +
+![]() +��+
+��+![]() ��
��
����������������ֻ������n�ηָ�ͼ����ͼ�ϱ�ע��Ӱ�����������д��̽�����̣�

������⣺����![]() +
+![]() +
+![]() +��+
+��+![]() ��
��
��ֻ�軭����n�ηָ�ͼ����ͼ�ϱ�ע��Ӱ��������������������գ�
���ݵ�n�ηָ�ͼ�ɵõ�ʽ��_________��
���ԣ�![]() +
+![]() +
+![]() +��+
+��+![]() =________��
=________��
�ع�Ӧ�ã�����![]() +
+![]() +
+![]() +��+
+��+![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
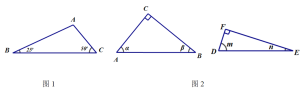
����Ŀ������ͼ1����һ�������Σ������ڽǷֱ�Ϊ��25��,50��,105���������������ηֳ���������������.������ָ��ʾ��ͼ����ע��Ҫ�ĽǶȡ�
����ͼ2��������ֱ�������Σ���ͼ��ʾ����C=��F=90�㣬��A, ��B, ��D, ��E�Ķ����ֱ���![]() �����ǻ�����ȡ����㽫�����������ηֱ�ָ�����������Σ�ʹ
�����ǻ�����ȡ����㽫�����������ηֱ�ָ�����������Σ�ʹ![]() ���ֳɵ�������������
���ֳɵ�������������![]() ���ֳɵ����������νǶȶ�Ӧ��ȡ�������ָ��ʾ��ͼ������ĸ��ע��Ҫ�ĽǶȡ�
���ֳɵ����������νǶȶ�Ӧ��ȡ�������ָ��ʾ��ͼ������ĸ��ע��Ҫ�ĽǶȡ�
����ͼ3����������![]() ����ƽ������һ��
����ƽ������һ��![]() ��ʹ�����������е�ÿһ�������ɵ������ξ�Ϊ���������Σ������ĵ���________��.
��ʹ�����������е�ÿһ�������ɵ������ξ�Ϊ���������Σ������ĵ���________��.
����ͼ4���ڵȱߡ�ABC����ƽ������һ��Q��ʹ����ȱ��������е�ÿһ�������ɵ������ξ�Ϊ���������Σ������ĵ���________��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ϵ�У��ڱ߳�Ϊ1�������������У���AOB�Ķ�����ڸ���ϣ���A��B������ֱ���A��3��1����B��2��3����
��1������ͼ�л�����AOB����y��ĶԳơ�A��OB�䣬��A�������Ϊ��������B�������Ϊ������
��2����д��A������x��ĶԳƵ�A��'������Ϊ������
��3�����A��OB��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����A��D��y���������ϣ���B��C�ֱ���x���ϣ�CDƽ�֡�ACB����y�ύ��D�㣬��CAO=90��-��BDO.
��1����֤��AC=BC��
��2����ͼ2����C������Ϊ��4��0������EΪAC��һ�㣬�ҡ�DEA=��DBO����BC+EC�ij���

��3����ͼ3����D��DF��AC��F�㣬��HΪFC��һ���㣬��GΪOC��һ���㣬��H��FC���ƶ�����G��OC���ƶ�ʱ��ʼ�������GDH=��GDO+��FDH�����ж�FH��GH��OG������֮���������ϵ��д����Ľ��۲�����֤��.
 ��ͼ3��
��ͼ3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬѧ�ǣ�ѧϰ��������֮�������Ѿ�����������������ʵ���ķ�Χ����˵�����ǵ�֪ʶԽ��Խ�ḻ�ˣ����ǣ�������������һ��ʲô�������أ������������ڼ��������ͼ������ʶһ��������.
��1����ͼ�١�ABC��һ���߳�Ϊ2�ĵ���ֱ�������Σ����������2����������б�ߵĸ�����ƴ����ͼ�ڵ�������ABCD������������ε����Ҳ�͵��������ε������Ϊ2������������εı߳�����![]() ������һ��������.
������һ��������.
��2����ͼ��ֱ��Ϊ1����λ���ȵ�Բ��ԭ��O���������ҹ���һ�ܣ�Բ�ϵ�һ��P������ʱ���O�غϣ���ԭ�㵽���O������OO���ij��Ⱦ͵���Բ���ܳ�![]() �����������ϵ�O��������ʵ������_____������һ��������.
�����������ϵ�O��������ʵ������_____������һ��������.

��3����ͼ����Rt��ABC�У���C=90����AC=2��BC=1��������֪�����AB=_____������һ��������.���ˣ����Ŵ�Ҷ��������Dz������˸��������ʶ�ˣ���ô��Ҳ������ͼ�������������������ɣ�

��������6��8������ͼ�У�ÿ��С�����α߳���Ϊ1��������һ����Ϊ![]() ���߶���
���߶���

��ѧϰ��ʵ��������֪�������ϵĵ���ʵ����һһ��Ӧ�Ĺ�ϵ����ô�������������ҵ���ʾ��![]() �ĵ���
�ĵ���
![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com