
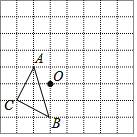
【题目】在如图所示的方格纸中,每个小方格都是边长为1个单位长度的正方形,△ABC的顶点及点O都在格点上(每个小方格的顶点叫做格点).
(1)以点O为位似中心,在网格区域内画出△A′B′C′,使△A′B′C′与△ABC位似(A′、B′、C′分别为A、B、C的对应点),且位似比为2:1;
(2)△A′B′C′的面积为 个平方单位;
(3)若网格中有一格点D′(异于点C′),且△A′B′D′的面积等于△A′B′C′的面积,请在图中标出所有符合条件的点D′.(如果这样的点D′不止一个,请用D1′、D2′、…、Dn′标出)
科目:初中数学 来源: 题型:
【题目】天门山索道是世界最长的高山客运索道,位于张家界天门山景区.在一次检修维护中,检修人员从索道A处开始,沿A﹣B﹣C路线对索道进行检修维护.如图:已知![]() 米,
米,![]() 米,AB与水平线
米,AB与水平线![]() 的夹角是
的夹角是![]() ,BC与水平线
,BC与水平线![]() 的夹角是
的夹角是![]() .求:本次检修中,检修人员上升的垂直高度
.求:本次检修中,检修人员上升的垂直高度![]() 是多少米?(结果精确到1米,参考数据:
是多少米?(结果精确到1米,参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AB=AC,以AB为直径作⊙O,分别交BC于点D,交CA的延长线于点E,过点D作
中,AB=AC,以AB为直径作⊙O,分别交BC于点D,交CA的延长线于点E,过点D作![]() 于点H,连接DE交线段OA于点F.
于点H,连接DE交线段OA于点F.
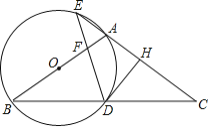
(1)试猜想直线DH与⊙O的位置关系,并说明理由;
(2)若AE=AH,EF=4,求DF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
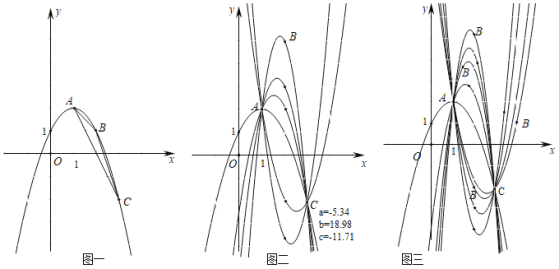
【题目】定义:连接抛物线上两点的线段叫抛物线的弦,在这两点之间抛物线上的任意一点P与此两点构成的三角形称作抛物线的弦三角,点P称作弦锥,设点P的横坐标为x.
已知抛物线经过A(1,2)、B(m,n)、C(3,﹣2)三点,P是抛物线上AC之间的一点,以AC为弦的弦三角为△PAC.
(1)图一,当m=2,n=1时,求该抛物线的解析式,若x=k1时△PAC的面积最大,求k1的值.
(2)图二,当m=2,n≠1时,用n表示该抛物线的解析式,若x=k2时△PAC的面积最大,求k2的值.k1与k2有何数量关系?
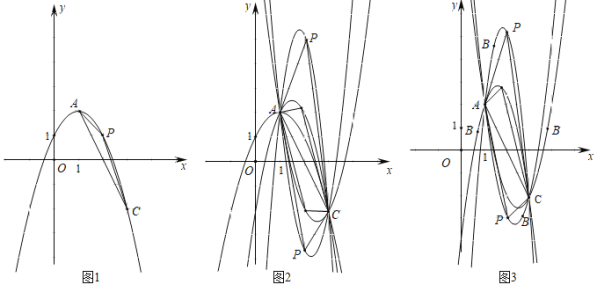
(3)图三,当m≠2,n≠1时,用m,n表示该抛物线的解析式,若x=k3时△PAC的面积最大,求k3的值.观察图1,2,3,过定点A、C,根据B在各种不同位置所得计算结果,你发现通过两个定点的抛物线系中,以此两点为弦的弦三角的面积取得最大值时,弦锥的横坐标有何规律?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数
,1)在反比例函数![]() 的图象上.
的图象上.

(1)求反比例函数![]() 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP=![]() S△AOB,求点P的坐标;
S△AOB,求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
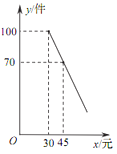
【题目】某商店购进一批成本为每件 30 元的商品,经调查发现,该商品每天的销售量 y(件)与销售单价 x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量 y 与销售单价 x 之间的函数关系式;
(2)若商店按单价不低于成本价,且不高于 50 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 w(元)最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润不低于 800 元,则每天的销售量最少应为多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.
(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为 ;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解).

查看答案和解析>>
科目:初中数学 来源: 题型:
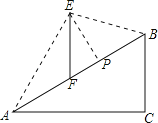
【题目】如图,在坡度i=1:![]() 的斜坡AB上立有一电线杆EF,工程师在点A处测得E的仰角为60°,沿斜坡前进20米到达B,此时测得点E的仰角为15°,现要在斜坡AB上找一点P,在P处安装一根拉绳PE来固定电线杆,以使EF保持竖直,为使拉绳PE最短,则FP的长度约为_____.(参考数据:
的斜坡AB上立有一电线杆EF,工程师在点A处测得E的仰角为60°,沿斜坡前进20米到达B,此时测得点E的仰角为15°,现要在斜坡AB上找一点P,在P处安装一根拉绳PE来固定电线杆,以使EF保持竖直,为使拉绳PE最短,则FP的长度约为_____.(参考数据:![]() =1.414,
=1.414,![]() =1.732)
=1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠F的度数是( )
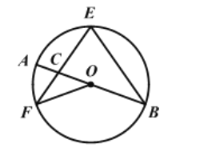
A.20°B.35°C.40°D.55°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com