
【题目】已知:△ABC是等腰直角三角形.∠A=90°,CE平分∠ACB交AB于点E.
(1)如图1,若点D在斜边BC上,DM垂直平分BE,垂足为M.求证:BD=AE.
(2)如图2,过点B作BF⊥CE交CE的延长线于点F.若CE=6,求△BEC的面积.

【答案】(1)见解析;(2)9
【解析】
(1)由∠BAC=90°,AB=AC,可得∠B=45°,由DM垂直平分BE,可得BD=DE,进而判断△BDE是等腰直角三角形,所以ED⊥BD,然后由角平分线的性质可得ED=AE,根据等量代换可得BD=AE;
(2)延长BF,CA,交与点G,由CE平分∠ACB,可得∠ACE=∠BCE,由BF⊥CE,可得∠BFC=∠GFC=90°,然后由三角形内角和定理可得:∠GBC=∠G,进而可得BC=GC,然后由等腰三角形的三线合一,可得BF=FG=![]() BG,所以BG=2BF=2FG=4,然后再由ASA,可证△ACE≌△ABG,可得EC=BG=4,最后根据三角形的面积公式即可求△BEC的面积.
BG,所以BG=2BF=2FG=4,然后再由ASA,可证△ACE≌△ABG,可得EC=BG=4,最后根据三角形的面积公式即可求△BEC的面积.
解:(1)∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵DM垂直平分BE,
∴BD=ED,
∴∠BED=∠B=45°,
∴∠EDC=∠B+∠BED=90°,
∵CE平分∠ACB,∠BAC=90°,∠EDC=90°,
∴ED=EA,
∴BD=AE;
(2)延长BF和CA交于点G,如图,
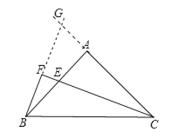
∵CE平分∠ACB,∴∠ACF=∠BCF,
∵BF⊥CE,∴∠BFC=∠GFC=90°,
∴∠CBG=∠CGB,∴CG=CB,
∴BF=GF=![]() BG,
BG,
∵∠GFC=∠GAB=90°,∴∠ACF+∠G=90°,
∴∠ABG+∠G=90°,∴∠ACF=∠ABG,
在△ACE和△ABG中,
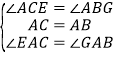 ,
,
∴△ACE≌△ABG(ASA),
∴CE=BG,
∴CE=2BF,
∵CE=6,
∴BF=![]() CE=3,
CE=3,
S△BEC=![]() CEBF=
CEBF=![]() ×6×3=9.
×6×3=9.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
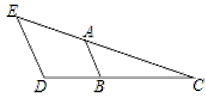
【题目】如图,∠E=50°,∠BAC=50°,∠D=110°,求∠ABD的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠E=50°,∠BAC=50°,(已知)
∴∠E= (等量代换)
∴ ∥ .( )
∴∠ABD+∠D=180°.( )
∴∠D=110°,(已知)
∴∠ABD=70°.(等式的性质)
查看答案和解析>>
科目:初中数学 来源: 题型:
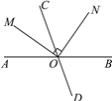
【题目】如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.
(1)若∠BOD=70°,求∠AOM和∠CON的度数;
(2)若∠BON=50°,求∠AOM和∠CON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax-2ax-3a(a<0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,抛物线的对称轴与抛物线交于点P,与直线BC交于点M,且PM= ![]() AB.
AB.
(1)求抛物线的解析式;
(2)点K是x轴正半轴上一点,点A、P关于点K的对称点分别为 ![]() 、
、 ![]() ,连接
,连接 ![]() 、
、 ![]() ,若
,若 ![]()
![]()
![]() ,求点K的坐标;
,求点K的坐标;
(3)矩形ADEF的边AF在x轴负半轴上,边AD在第二象限,AD=2,DE=3.将矩形ADEF沿x轴正方向平移t(t>0)个单位,直线AD、EF分别交抛物线于G、H.问:是否存在实数t,使得以点D、F、G、H为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图放置的△OAB1 , △B1A1B2 , △B2A2B3 , …都是边长为2的等边三角形,点A在y轴上,点O,B1 , B2 , B3…都在直线l上,则点B2017的坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC的底边长为8cm,腰长为5cm,一动点P在底边上从B向C以0.25cm/s的速度移动,请你探究:当P运动几秒时,P点与顶点A的连线PA与腰垂直。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S四边形DGOF=2:7.其中正确结论的个数是( ) 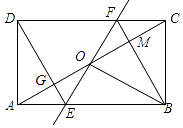
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=8.3海里,DE=30海里,且DE⊥EC,cos∠D= ![]() .
. 
(1)求小岛两端A、B的距离;
(2)过点C作CF⊥AB交AB的延长线于点F,求sin∠BCF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com