
分析 先对原式化简,再化简x与y,然后将化简后的x与y的值代入化简后的式子即可解答本题.
解答 解:$\frac{{x}^{2}-6xy+9{y}^{2}}{{x}^{3}-3{x}^{2}y}$÷($\frac{3}{x}$-$\frac{1}{y}$)
=$\frac{(x-3y)^{2}}{{x}^{2}(x-3y)}×\frac{xy}{3y-x}$
=$-\frac{y}{x}$,
∵x=2sin45°-2cos30°=2×$\frac{\sqrt{2}}{2}-2×\frac{\sqrt{3}}{2}$=$\sqrt{2}-\sqrt{3}$,
y=(-1)2013×(-$\frac{1}{2}$)-3+(sin50°-π)0-$\sqrt{(-9)^{2}}$+$\frac{1}{2}$$\sqrt{8}$=(-1)×(-8)+1-9+$\sqrt{2}$=8+1-9+$\sqrt{2}$=$\sqrt{2}$,
∴原式=$-\frac{\sqrt{2}}{\sqrt{2}-\sqrt{3}}=\sqrt{2}(\sqrt{3}+\sqrt{2})=\sqrt{6}+2$.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
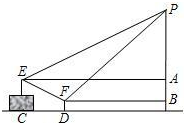 广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲乙二人分别站在E、F处,他们看气球的仰角分别为30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.5米,请问此气球有多高?(结果保留根号)
广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲乙二人分别站在E、F处,他们看气球的仰角分别为30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.5米,请问此气球有多高?(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在由边长为1的小正方形组成的10×10的网格中(组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A,B,C,D分别在网格的格点上.
如图,在由边长为1的小正方形组成的10×10的网格中(组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A,B,C,D分别在网格的格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
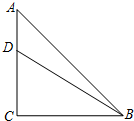 如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )
如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com