
【题目】在平面直角坐标系xOy中,⊙O的半径为r(r>0).给出如下定义:若平面上一点P到圆心O的距离d,满足![]() r,则称点P为⊙O的“随心点”.
r,则称点P为⊙O的“随心点”.
(1)当⊙O的半径r=2时,A(4,0),B(0,3),C(![]() ,﹣
,﹣![]() ),D(﹣
),D(﹣![]() ,﹣2)中,⊙O的“随心点”是 ;
,﹣2)中,⊙O的“随心点”是 ;
(2)若点E(6,8)是⊙O的“随心点”,求⊙O的半径r的取值范围;
(3)当⊙O的半径r=4时,直线y=﹣x+b(b≠0)与x轴交于点M,与y轴交于点N,若线段MN上存在⊙O的“随心点”,直接写出b的取值范围 .
【答案】(1)B,D;(2)![]() ≤r≤20;(3)2≤b≤6
≤r≤20;(3)2≤b≤6![]() 或﹣6
或﹣6![]() ≤b≤﹣2
≤b≤﹣2
【解析】
(1)分别判断A、B、C、D四个点到圆心O的距离是否符合规定即可;
(2)先算出OE长度,再根据“随心点“的定义列出不等式组解出r的取值范围;
(3)r已知,因此先算出![]() r和
r和![]() r的值,由解析式y=﹣x+b可得M、N坐标,由于直线y=x与y=﹣x+b垂直,故联立两直线方程可解出交点P的坐标,然后用两点间的距离公式可得OP长度(注意b的符号未知,表示长度应加绝对值符号),线段MN上存在“随心点“,则意味着OM≥2且OP≤6,列出不等式组即可解出b的取值范围.
r的值,由解析式y=﹣x+b可得M、N坐标,由于直线y=x与y=﹣x+b垂直,故联立两直线方程可解出交点P的坐标,然后用两点间的距离公式可得OP长度(注意b的符号未知,表示长度应加绝对值符号),线段MN上存在“随心点“,则意味着OM≥2且OP≤6,列出不等式组即可解出b的取值范围.
解:(1)∵r=2,
∴![]() r=1,
r=1,![]() r=3,
r=3,
∵A(4,0),
∴OA=4>3,
∴A不是“随心点”;
∵B(0,3),
∴OB=3,
∴B是“随心点”;
∵C(![]() ,﹣
,﹣![]() ),
),
∴OC=![]() =
=![]() <1,
<1,
∴C不是“随心点”;
∵D(﹣![]() ,﹣2),
,﹣2),
∴OD=![]() =
=![]() ,
,
∴D是“随心点”;
综上所述,⊙O的“随心点”是B、D,
故答案为:B、D;
(2)∵E(6,8),
∴OE=![]() =10,
=10,
因为E是⊙O的“随心点”,
∴![]() r≤OE≤
r≤OE≤![]() r,即
r,即![]() r≤10≤
r≤10≤![]() r,
r,
解得![]() ≤r≤20;
≤r≤20;
(3)∵r=4,
∴![]() r=2,
r=2,![]() r=6,
r=6,
直线y=﹣x+b(b≠0)与x轴交于点M,与y轴交于点N,
∴M(b,0),N(0,b),
过点O且与直线y=﹣x+b垂直的直线解析式为y=x,
联立方程组:![]() ,解得:
,解得:![]() ,
,
∴直线y=﹣x+b与直线y=x交点坐标为P(![]() ,
,![]() ),
),
∴OP=![]() ,
,
∵线段MN上存在⊙O的随心点,
∴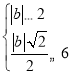 ,
,
解得2≤b≤6![]() 或﹣6
或﹣6![]() ≤b≤﹣2.
≤b≤﹣2.


科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=![]() BC,连接CD和EF.
BC,连接CD和EF.
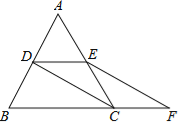
(1)求证:DE=CF;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点E在BC边上.AE=AB,将线段AC绕点A旋转到AF的位置.使得∠CAF=∠BAE.连接EF,EF与AC交于点G.

(1)求证:EF =BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形![]() 是平行四边形,
是平行四边形,![]() ,若
,若![]() ,
,![]() 的长是关于
的长是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,且
的两个根,且![]() .
.
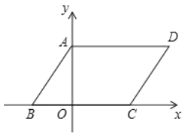
(1)直接写出:![]() ______,
______,![]() ______;
______;
(2)若点![]() 为
为![]() 轴正半轴上的点,且
轴正半轴上的点,且![]() ;
;
①求经过![]() ,
,![]() 两点的直线解析式;
两点的直线解析式;
②求证:![]() .
.
(3)若点![]() 在平面直角坐标系内,则在直线
在平面直角坐标系内,则在直线![]() 上是否存在点
上是否存在点![]() ,使以
,使以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形?若存在,直接写出
为顶点的四边形为菱形?若存在,直接写出![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
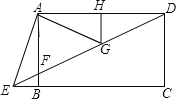
【题目】如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点.
(1)求证:AE=AG;
(2)若BE=2,BF=1,AG=5,点H是AD的中点,求GH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
如图1.在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,可以得到:
![]()
证明:过点A作AD⊥BC,垂足为D.
在Rt△ABD中,![]()
∴![]()
∴![]()
同理:![]()
![]()
∴![]()
(1)通过上述材料证明:
![]()
(2)运用(1)中的结论解决问题:
如图2,在![]() 中,
中,![]() ,求AC的长度.
,求AC的长度.
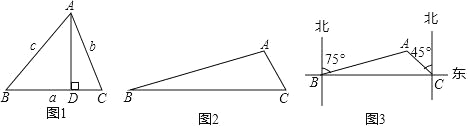
(3)如图3,为了开发公路旁的城市荒地,测量人员选择A、B、C三个测量点,在B点测得A在北偏东75°方向上,沿笔直公路向正东方向行驶18km到达C点,测得A在北偏西45°方向上,根据以上信息,求A、B、C三点围成的三角形的面积.
(本题参考数值:sin15°≈0.3,sin120°≈0.9,![]() ≈1.4,结果取整数)
≈1.4,结果取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行
销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)于销售单价x(元
/个)之间的对应关系如图所示.
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查销售规律,求利润w(元)与销售单价x(元/个)之间的
函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试求此时这种许愿瓶的销售单价,并求出
最大利润.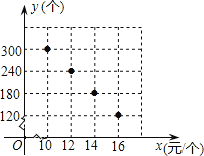
查看答案和解析>>
科目:初中数学 来源: 题型:
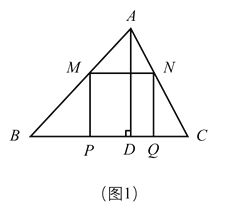
【题目】如图在锐角![]() 中,
中,![]() ,高
,高![]() ,两动点
,两动点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上滑动(不包含端点),且
上滑动(不包含端点),且![]() ,以
,以![]() 为边长向下作正方形
为边长向下作正方形![]() ,设
,设![]() ,正方形
,正方形![]() 与
与![]() 公共部分的面积为
公共部分的面积为![]() .
.
(1)如图(1),当正方形![]() 的边
的边![]() 恰好落在
恰好落在![]() 边上时,求
边上时,求![]() 的值.
的值.
(2)如图(2),当![]() 落
落![]() 外部时,求出
外部时,求出![]() 与
与![]() 的函数关系式(写出
的函数关系式(写出![]() 的取值范围)并求出
的取值范围)并求出![]() 为何值时
为何值时![]() 最大,最大是多少?
最大,最大是多少?
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com