
【题目】在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行
销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)于销售单价x(元
/个)之间的对应关系如图所示.
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查销售规律,求利润w(元)与销售单价x(元/个)之间的
函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试求此时这种许愿瓶的销售单价,并求出
最大利润.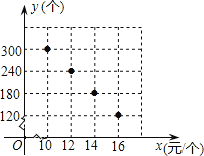
【答案】(1)y是x的一次函数,y=-30x+600(2)w=-30x2+780x-3600(3)以15元/个的价格销售这批许愿瓶可获得最大利润1350元
【解析】
(1)观察可得该函数图象是一次函数,设出一次函数解析式,把其中两点代入即可求得该函数解析式,进而把其余两点的横坐标代入看纵坐标是否与点的纵坐标相同.
(2)销售利润=每个许愿瓶的利润×销售量.
(3)根据进货成本可得自变量的取值,结合二次函数的关系式即可求得相应的最大利润.
解:(1)y是x的一次函数,设y=kx+b,
∵图象过点(10,300),(12,240),
∴![]() ,解得
,解得![]() .∴y=-30x+600.
.∴y=-30x+600.
当x=14时,y=180;当x=16时,y=120,
∴点(14,180),(16,120)均在函数y=-30x+600图象上.
∴y与x之间的函数关系式为y=-30x+600.
(2)∵w=(x-6)(-30x+600)=-30x2+780x-3600,
∴w与x之间的函数关系式为w=-30x2+780x-3600.
(3)由题意得:6(-30x+600)≤900,解得x≥15.
w=-30x2+780x-3600图象对称轴为:![]() .
.
∵a=-30<0,∴抛物线开口向下,当x≥15时,w随x增大而减小.
∴当x=15时,w最大=1350.
∴以15元/个的价格销售这批许愿瓶可获得最大利润1350元.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】某健身器材公司销售A,B两款跑步机,这两款跑步机的进价和售价如下表所示:
| A | B |
进价 | 4500 | 6200 |
售价 | 6000 | 8000 |
该公司计划购进两款跑步机若干台,共需![]() 万元,全部销售后可获利
万元,全部销售后可获利![]() 万元.
万元.
![]() 问该公司计划购进A,B两款跑步机各多少台?
问该公司计划购进A,B两款跑步机各多少台?
![]() 为了适应市场需求的变化,该公司决定在原计划的基础上,减少A款跑步机的购进数量,增加B款跑步机的购进数量,已知B款跑步机增加的数量是A款跑步机减少的数量的2倍.若用于购进这两种款跑步机的总资金不超过29.6万元,问A种款跑步机购进数量至多减少多少台?
为了适应市场需求的变化,该公司决定在原计划的基础上,减少A款跑步机的购进数量,增加B款跑步机的购进数量,已知B款跑步机增加的数量是A款跑步机减少的数量的2倍.若用于购进这两种款跑步机的总资金不超过29.6万元,问A种款跑步机购进数量至多减少多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙O的半径为r(r>0).给出如下定义:若平面上一点P到圆心O的距离d,满足![]() r,则称点P为⊙O的“随心点”.
r,则称点P为⊙O的“随心点”.
(1)当⊙O的半径r=2时,A(4,0),B(0,3),C(![]() ,﹣
,﹣![]() ),D(﹣
),D(﹣![]() ,﹣2)中,⊙O的“随心点”是 ;
,﹣2)中,⊙O的“随心点”是 ;
(2)若点E(6,8)是⊙O的“随心点”,求⊙O的半径r的取值范围;
(3)当⊙O的半径r=4时,直线y=﹣x+b(b≠0)与x轴交于点M,与y轴交于点N,若线段MN上存在⊙O的“随心点”,直接写出b的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知A(2t,0),B(0,-2t),C(2t,4t)三点,其中t>0,函数![]() 的图象分别与线段BC,AC交于点P,Q.若S△PAB-S△PQB=t,则t的值为__.
的图象分别与线段BC,AC交于点P,Q.若S△PAB-S△PQB=t,则t的值为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数y=![]() (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,AB为直径,C为⊙O上一点.

(1)如图1,过点C作⊙O的切线,与AB延长线相交于点P,若∠CAB=27°,求∠P的度数;
(2)如图2,D为弧AB上一点,OD⊥AC,垂足为E,连接DC并延长,与AB的延长线交于点P,若∠CAB=10°,求∠P的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6 000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”越来越受到人们的关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:

(1)接受问卷调查的学生共有______人,条形统计图中m的值为______;
(2)扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为______;
(3)若该中学共有学生1800人,根据上述调查结果,可以估计出该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为______人;
(4)若从对校园安全知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加校园安全知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com