
分析 由外接圆的圆心在斜边的中点上即可求出外接圆的半径;利用内切圆半径等于两直角边的和与斜边的差的一半,即可计算出内切圆半径.
解答 解:∵直角三角形的两条直角边长分别为a和b,斜长为c,
∴外接圆的半径=$\frac{c}{2}$,内切圆的半径=$\frac{a+b-c}{2}$.
故答案为:$\frac{c}{2}$,$\frac{a+b-c}{2}$.
点评 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心;三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.也考查了三角形的外心性质.记住直角三角形的外接圆半径R和内切圆半径r之间的数量关系是解题关键.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | -2 | -1 | 0 | 1 | 2 |
| y | 12 | 10 | 8 | 6 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
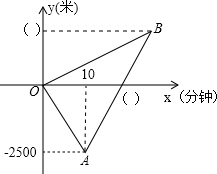 早上小芳和妈妈同时从家里出发,小芳步行上学、妈妈骑自行车上班,两人的行进方向正好相反,规定从家往学校的方向为正,如图是她们离家的距离y(米)与时间x(分钟)之间的函数图象,妈妈骑车走了10分钟时接到小芳的电话,立即以原速度前往学校,若已知小芳步行的速度为50米/分钟,并且妈妈与小芳同时到达学校.
早上小芳和妈妈同时从家里出发,小芳步行上学、妈妈骑自行车上班,两人的行进方向正好相反,规定从家往学校的方向为正,如图是她们离家的距离y(米)与时间x(分钟)之间的函数图象,妈妈骑车走了10分钟时接到小芳的电话,立即以原速度前往学校,若已知小芳步行的速度为50米/分钟,并且妈妈与小芳同时到达学校.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
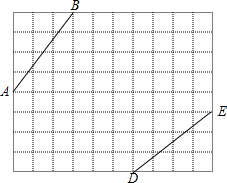 如图所示,是10×8的正方形网格,网格中的每个小正方形的边长都是1,线段AB和线段DE的端点都在小正方形的顶点上.
如图所示,是10×8的正方形网格,网格中的每个小正方形的边长都是1,线段AB和线段DE的端点都在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
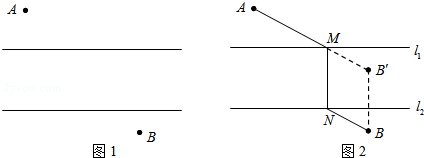
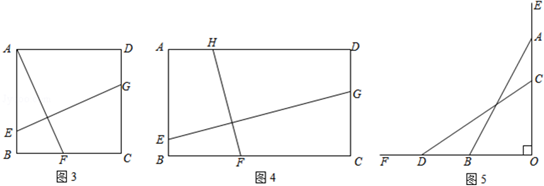
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com