
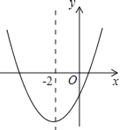
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,顶点坐标为(-2,-9a),下列结论:①abc>0;②4a+2b+c<0;③9a-b+c=0;④若方程a(x+5)(x-1)=-1有两个根x1和x2,且x1<x2,则-5<x1<x2<1;⑤若方程|ax2+bx+c|=1有四个根,则这四个根的和为-8,其中正确的结论有( )个.
A.2B.3C.4D.5
【答案】B
【解析】
根据开口方向及顶点坐标求出b=4a,c=-5a,可求得①②③,根据图像得平移和韦达定理即可判断④⑤.
解:函数的顶点坐标为(-2,-9a)
则![]() ,
,![]()
则b=4a,c=-5a
函数开口向上,
a>0,
则b>0,c<0
则abc<0,①错误
把x=2代入二次函数表达式,则
![]() =7a>0,②错误
=7a>0,②错误
![]() =0,③正确
=0,③正确
a(x+5)(x-1)=-1展开后得
![]()
函数![]() 向上平移一个单位变成
向上平移一个单位变成
![]() =
=![]()
其与x轴的两个交点的横坐标![]() 和
和![]() 就是方程
就是方程
![]() 的两个解
的两个解
而![]() 与x轴的交点的坐标为(-5,0),(1,0)
与x轴的交点的坐标为(-5,0),(1,0)
因为y=![]() 在
在![]() 的上方,
的上方,
所以-5<![]() <
<![]() <1,④正确
<1,④正确
![]() 化简为
化简为
![]() 或
或![]()
![]() 的两解为
的两解为![]() 和
和![]()
由韦达定理
![]() +
+![]() =
=![]() =-4
=-4
![]() 的两个解设为
的两个解设为![]() 和
和![]()
由韦达定理
![]() +
+![]() =
=![]() =-4
=-4
故![]() +
+![]() +
+![]() +
+![]() =-8,⑤正确
=-8,⑤正确
故本题答案为B.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】在下列函数图象上任取不同两点P1(x1,y1)、P2(x2,y2),一定能使![]() <0成立的是( )
<0成立的是( )
A.y=3x﹣1(x<0)B.y=﹣x2+2x﹣1(x>0)
C.y=﹣![]() (x>0)D.y=x2﹣4x+1(x<0)
(x>0)D.y=x2﹣4x+1(x<0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数
,1)在反比例函数![]() 的图象上.
的图象上.

(1)求反比例函数![]() 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP=![]() S△AOB,求点P的坐标;
S△AOB,求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
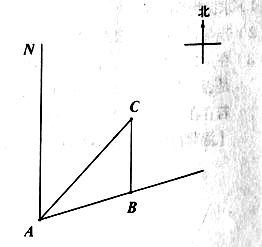
【题目】如图,一艘船以每小时30海里的速度向北偏东75°方向航行,在点![]() 处测得码头
处测得码头![]() 的船的东北方向,航行40分钟后到达
的船的东北方向,航行40分钟后到达![]() 处,这时码头
处,这时码头![]() 恰好在船的正北方向,在船不改变航向的情况下,求出船在航行过程中与码头
恰好在船的正北方向,在船不改变航向的情况下,求出船在航行过程中与码头![]() 的最近距离.(结果精确的0.1海里,参考数据
的最近距离.(结果精确的0.1海里,参考数据![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
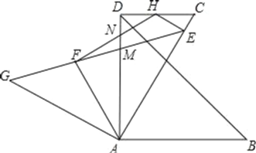
【题目】如图,将等腰Rt△GAE绕点A顺时针旋转60°得到△DAB,其中∠GAE=∠DAB=90°,GE与AD交于点M,过点D作DC∥AB交AE于点C.已知AF平分∠GAM,EH⊥AE交DC于点H,连接FH交DM于点N,若AC=2![]() ,则MN的值为______.
,则MN的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的顶点B在⊙O上. AC经过圆心0并与圆相交于点D,C,过C作直线CE丄AB,交AB的延长线于点E,且CB平分∠ACE.
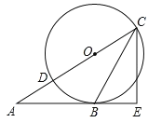
(1)求证:AB是圆O的切线;
(2)若BE=3,CE=4,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校八年级共400名学生,为了解该年级学生的视力情况,从中随机抽取40名学生的视力数据作为样本,数据统计如下:
4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.1 5.2
5.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.2
4.4 4.2 4.3 5.3 4.9 5.2 4.9 4.8 4.6 5.1
4.2 4.4 4.5 4.1 4.5 5.1 4.4 5.0 5.2 5.3
根据数据绘制了如下的表格和统计图:
等级 | 视力(x) | 频数 | 频率 |
|
| 4 | 0.1 |
|
| 12 | 0.3 |
|
|
| |
|
|
| |
| 10 | 0.25 | |
合计 | 40 | 1 | |
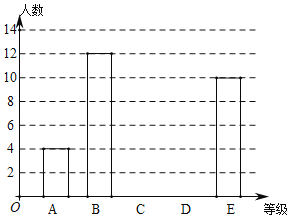
根据上面提供的信息,回答下列问题:
(1)统计表中的![]() ,
,![]() ;
;
(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该校八年级学生视力为“![]() 级”的有多少人?
级”的有多少人?
(4)该年级学生会宣传部有2名男生和2名女生,现从中随机挑选2名同学参加“防控近视,爱眼护眼”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠BAC=20°,点O是AB的中点,将OB绕点O顺时针旋转α角时(0°<α<180°),得到OP,当△ACP为等腰三角形时,α的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com