
【题目】如图,将等腰Rt△GAE绕点A顺时针旋转60°得到△DAB,其中∠GAE=∠DAB=90°,GE与AD交于点M,过点D作DC∥AB交AE于点C.已知AF平分∠GAM,EH⊥AE交DC于点H,连接FH交DM于点N,若AC=2![]() ,则MN的值为______.
,则MN的值为______.
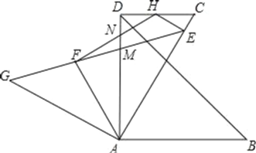
【答案】9﹣5![]() .
.
【解析】
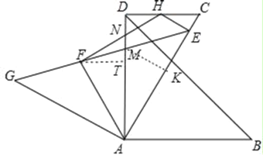
作MK⊥AC,FT⊥AD垂足分别为K,T,证明△AGF≌△AEM,△AFT≌△AMK得到AF=AM,FT=MK=EK=DM,在RT△ADC中根据已知条件求出CD,AD,设MK=EK=x,根据AE=AK+EK列出方程求出x,在RT△HEC中求出HC,进而求出DH,再根据![]() =
=![]() ,求出DN,利用MN=AD﹣AM﹣DN求出MN.
,求出DN,利用MN=AD﹣AM﹣DN求出MN.
解:作MK⊥AC,FT⊥AD垂足分别为K,T,
∵Rt△GAE绕点A顺时针旋转60°得到△DAB,
∴∠GAD=∠CAB=60°,
∵∠GAE=∠DAB=90°,AG=AE=AD=AB,
∴∠DAC=30°,∠G=∠AEG=45°,
∵AF平分∠GAD,
∴∠GAF=∠FAT=30°,
在△AGF和△AEM中,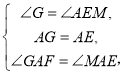
∴△AGF≌△AEM,
∴AF=AM
在△AFT和△AMK中,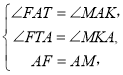
∴△AFT≌△AMK,
∴AT=AK,
∵AD=AE,
∴DT=EK,
∵∠KME=∠KEM=45°,
∴MK=EK=DT=FT,
设MK=KE=x,则AK=![]() x,
x,
∵AC=2![]() ,∠DAC=30°,
,∠DAC=30°,
∴DC=![]() ,AD=3,∴AE=AD=3,
,AD=3,∴AE=AD=3,
∴x+![]() x=3
x=3
x= ,
,
∴DT=DM=FH=MK=EK= ,AM=3(
,AM=3(![]() ﹣1),EC=2
﹣1),EC=2![]() ﹣3,
﹣3,
在RT△HEC中,∵∠C=60°,EC=2![]() ﹣3,
﹣3,
∴HC=2EC=4![]() ﹣6,DH=DC﹣HC=
﹣6,DH=DC﹣HC=![]() ﹣(4
﹣(4![]() ﹣6)=6﹣3
﹣6)=6﹣3![]() ,
,
设DN=y,∵DH∥FT,
∴![]() =
=![]() ,
,
∴y=2![]() ﹣3,
﹣3,
∴MN=AD﹣AM﹣DN=3﹣3(![]() ﹣1)﹣(2
﹣1)﹣(2![]() ﹣3)=9﹣5
﹣3)=9﹣5![]() .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
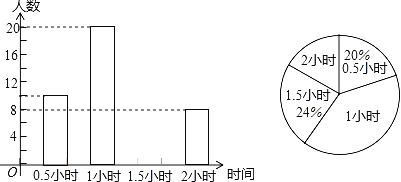
(1)在这次调查中共调查了多少名学生;
(2)求户外活动时间为1.5小时的人数,并补充频数分布直方图;
(3)求户外活动时间的众数和中位数是多少;
(4)本次调查中学生参加户外活动的平均时间是否符合要求,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg,且不高于180元/kg,经销一段时间后得到如下数据:

设y与x的关系是我们所学过的某一种函数关系.
(1)写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+2x﹣3与x轴交于A,B两点(点A在点B的左侧),将这条抛物线向右平移m(m>0)个单位长度,平移后的抛物线与x轴交于C,D两点(点C在点D的左侧),若B,C是线段AD的三等分点,则m的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c和直线y=x+1交于A,B两点,点A在x轴上,点B在直线x=3上,直线x=3与x轴交于点C

(1)求抛物线的解析式;
(2)点P从点A出发,以每秒![]() 个单位长度的速度沿线段AB向点B运动,点Q从点C出发,以每秒2个单位长度的速度沿线段CA向点A运动,点P,Q同时出发,当其中一点到达终点时,另一个点也随之停止运动,设运动时间为t秒(t>0).以PQ为边作矩形PQNM,使点N在直线x=3上.
个单位长度的速度沿线段AB向点B运动,点Q从点C出发,以每秒2个单位长度的速度沿线段CA向点A运动,点P,Q同时出发,当其中一点到达终点时,另一个点也随之停止运动,设运动时间为t秒(t>0).以PQ为边作矩形PQNM,使点N在直线x=3上.
①当t为何值时,矩形PQNM的面积最小?并求出最小面积;
②直接写出当t为何值时,恰好有矩形PQNM的顶点落在抛物线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,顶点坐标为(-2,-9a),下列结论:①abc>0;②4a+2b+c<0;③9a-b+c=0;④若方程a(x+5)(x-1)=-1有两个根x1和x2,且x1<x2,则-5<x1<x2<1;⑤若方程|ax2+bx+c|=1有四个根,则这四个根的和为-8,其中正确的结论有( )个.
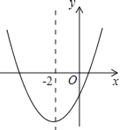
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年5月的第二个星期日即为母亲节,“父母恩深重,恩怜无歇时”,许多市民喜欢在母亲节为母亲送花,感恩母亲,祝福母亲.今年节日前夕,某花店采购了一批康乃馨,经分析上一年的销售情况,发现这种康乃馨每天的销售量y(支)是销售单价x(元)的一次函数,已知销售单价为7元/支时,销售量为16支;销售单价为8元/支时,销售量为14支.
(1)求这种康乃馨每天的销售量y(支)关于销售单价x(元/支)的一次函数解析式;
(2)若按去年方式销售,已知今年这种康乃馨的进价是每支5元,商家若想每天获得42元的利润,销售单价要定为多少元?
(3)在(2)的条件下,当销售单价x为何值时,花店销售这种康乃馨每天获得的利润最大?并求出获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠B=90°,AB=4,BC=2,点D、E分别是边BC、AC的中点,连接DE.将△CDE绕点C逆时针方向旋转,记旋转角为α.
(1)问题发现
①当α=0°时,![]() =_______;
=_______;
②当α=180°时,![]() =______.
=______.
(2)拓展探究
试判断:当0°≤α<360°时,![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
△CDE绕点C逆时针旋转至A、B、E三点在同一条直线上时,求线段BD的长.
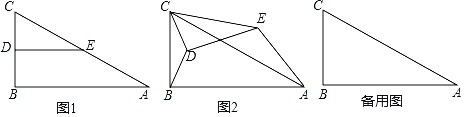
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,∠ABD=60°,点E从点A出发,以每秒2个单位长度的速度沿边AB运动,到点B停止运动.过点E作EF∥BD交AD于点F,将△AEF绕点E顺时针旋转得到△GEH,且点G落在线段EF上,设点E的运动时间为t(秒)(0<t<3).
(1)若t=1,求△GEH的面积;
(2)若点G在∠ABD的平分线上,求BE的长;
(3)设△GEH与△ABD重叠部分的面积为T,用含t的式子表示T,并直接写出当0<t<3时T的取值范围.
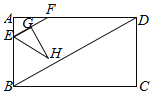
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com