
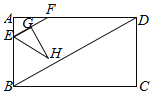
【题目】如图,矩形ABCD中,AB=6,∠ABD=60°,点E从点A出发,以每秒2个单位长度的速度沿边AB运动,到点B停止运动.过点E作EF∥BD交AD于点F,将△AEF绕点E顺时针旋转得到△GEH,且点G落在线段EF上,设点E的运动时间为t(秒)(0<t<3).
(1)若t=1,求△GEH的面积;
(2)若点G在∠ABD的平分线上,求BE的长;
(3)设△GEH与△ABD重叠部分的面积为T,用含t的式子表示T,并直接写出当0<t<3时T的取值范围.
【答案】(1)2![]() ;(2)3;(3)T=
;(2)3;(3)T=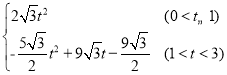 .
.
【解析】
(1)根据四边形ABCD是矩形和EF∥BD,可推出AE和AF的长,即可求出答案;
(2)由BG平分∠ABD,可得∠EBG=![]() ∠ABD=30°,再根据∠AEG=∠EBG+∠EGB=60°,可得∠EBG=∠EGB=30°,即可推出BE的长;
∠ABD=30°,再根据∠AEG=∠EBG+∠EGB=60°,可得∠EBG=∠EGB=30°,即可推出BE的长;
(3)当点H落在BD上时,作EJ⊥BD于J,根据EF∥BD,推出△EBH是等边三角形,从而得出t=1,再分当0<t≤1时和当1<t<3时两种情况讨论即可.
解:(1)如图1中,
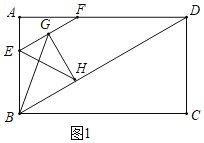
∵四边形ABCD是矩形,
∴∠A=90°,
∵EF∥BD,
∴∠AEF=60°,
∵AE=2,
∴AF=AEtan60°=![]() ,
,
∴S△EGH=S△AEF=![]() AEAF=
AEAF=![]() ×2×
×2×![]() =
=![]() ;
;
(2)如图2中,
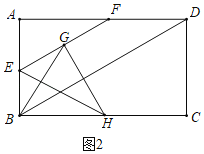
由题意得,BG平分∠ABD,
∴∠EBG=![]() ∠ABD=30°,
∠ABD=30°,
∵∠AEG=∠EBG+∠EGB=60°,
∴∠EBG=∠EGB=30°,
∴BE=EG=AE=3;
(3)如图1﹣1中,当点H落在BD上时,作EJ⊥BD于J,
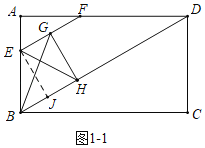
∵EF∥BD,
∴∠FEH=∠EHB=60°,
∴△EBH是等边三角形,
∴EH=EB=EF=2AE,
∴AE=2,BE=4,
∴t=1,
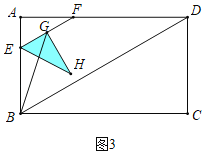
如图3中,当0<t≤1时,重叠部分是△EGH,T=S△AEF=![]() ×2t×2t×
×2t×2t×![]() =
=![]() t2,
t2,
如图4中,当1<t<3时,重叠部分是四边形MNGE,作EJ⊥BD于J,
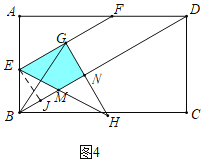
在Rt△EBJ中,∵BE=6﹣2t,∠EBJ=60°,
∴BJ=![]() BE=3﹣t,EJ=
BE=3﹣t,EJ=![]() BJ=3
BJ=3![]() ﹣
﹣![]() t,
t,
∵△EBM是等边三角形,
∴BJ=JM=3﹣t,
∵四边形EGNJ是矩形,
∴EG=NJ=2t,
∴MN=NJ﹣MJ=3t﹣3,
∴T=![]() (MN+EG)EJ=
(MN+EG)EJ=![]() (3t﹣3+2t)(3
(3t﹣3+2t)(3![]() ﹣
﹣![]() t)=
t)=![]() t2+9
t2+9![]() t
t![]() ,
,
综上所述,T=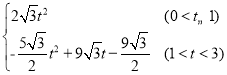 .
.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
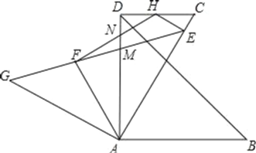
【题目】如图,将等腰Rt△GAE绕点A顺时针旋转60°得到△DAB,其中∠GAE=∠DAB=90°,GE与AD交于点M,过点D作DC∥AB交AE于点C.已知AF平分∠GAM,EH⊥AE交DC于点H,连接FH交DM于点N,若AC=2![]() ,则MN的值为______.
,则MN的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
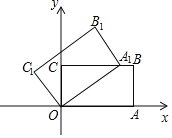
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为( )
A. (﹣![]() ) B. (﹣
) B. (﹣![]() ) C. (﹣
) C. (﹣![]() ) D. (﹣
) D. (﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明调查了本校九年级300名学生到校的方式,根据调査结果绘制出统计图的一部分如图:
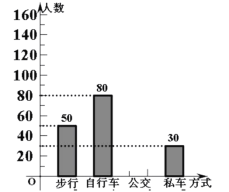
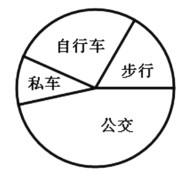
(1)补全条形统计图;
(2)求扇形统计图中表示“步行”的扇形圆心角的度数;
(3)请估计在全校1200名学生中乘公交的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
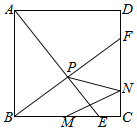
【题目】如图,正方形ABCD的边长为2,点E,点F分别是边BC,边CD上的动点,且BE=CF,AE与BF相交于点P.若点M为边BC的中点,点N为边CD上任意一点,则MN+PN的最小值等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
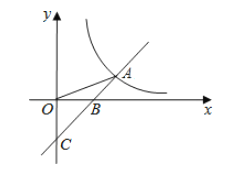
轴交于点![]() ,与反比例函数
,与反比例函数![]() 的图象在第一象限交于点
的图象在第一象限交于点![]() ,连接
,连接![]() ,且
,且![]() .则不等式
.则不等式![]() 的解集为( )
的解集为( )
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.-3<x<0或x>3
D.-3<x<0或x>3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解本校学生的预防新型冠状病毒知识的普及情况,从该校2000名学生中随机抽取了部分学生进行调查,调查结果按了解程度分为“非常了解”、“了解”、“了解较少”、“不了解”四类,并将调査结果绘制出以下两幅不完整的统计图,请根据统计图回答下列问题:

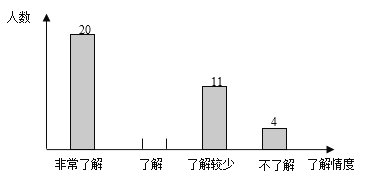
(1)本次调查的学生共有多少人?
(2)估计该校2000名学生中“了解”的人数约有多少人?
(3)若“不了解”的4人中有甲、乙两名男生,丙、丁两名女生,从这4人中随机抽取两人去重新参加预防新冠病毒如识培训,请用画树状图或列表的方法,求恰好抽到2名男生的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
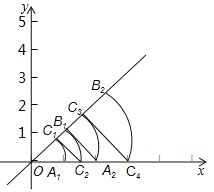
【题目】如图,已知直线l的表达式为y=x,点A1的坐标为(1,0),以O为圆心,OA1为半径画弧,与直线l交于点C1,记![]() 长为m1;过点A1作A1B1垂直x轴,交直线l于点B1,以O为圆心,OB1为半径画弧,交x轴于C2,记
长为m1;过点A1作A1B1垂直x轴,交直线l于点B1,以O为圆心,OB1为半径画弧,交x轴于C2,记![]() 的长为m2;过点B1作A2B1垂直l,交x轴于点A2,以O为圆心,OA2为半径画弧,交直线l于C3,记
的长为m2;过点B1作A2B1垂直l,交x轴于点A2,以O为圆心,OA2为半径画弧,交直线l于C3,记![]() 的长为m3…按照这样规律进行下去,mn的长为( )
的长为m3…按照这样规律进行下去,mn的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com