
【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg,且不高于180元/kg,经销一段时间后得到如下数据:

设y与x的关系是我们所学过的某一种函数关系.
(1)写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
【答案】(1)y=0.5x+160(120≤x≤180)(2)销售单价为180元时,销售利润最大,最大利润是7000元
【解析】
(1)首先由表格可知:销售单价每涨10元,就少销售5kg,即可得y与x是一次函数关系,则可求得答案;
(2)首先设销售利润为w元,根据题意可得二次函数,然后求最值即可.
(1)∵由表格可知:销售单价每涨10元,就少销售5kg,
∴y与x是一次函数关系,
∴y与x的函数关系式为:y=1000.5(x120)=0.5x+160,
∵销售单价不低于120元/kg.且不高于180元/kg,
∴自变量x的取值范围为:120≤x≤180;
(2)设销售利润为w元,
则w=(x80)(0.5x+160)=![]() x2+200x12800=
x2+200x12800=![]() (x200)2+7200,
(x200)2+7200,
∵a=![]() <0,
<0,
∴当x<200时,w随x的增大而增大,
∴当x=180时,销售利润最大,最大利润是:w=![]() (180200)2+7200=7000(元),
(180200)2+7200=7000(元),
答:当销售单价为180元时,销售利润最大,最大利润是7000元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图像与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
的图像与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
(1)求线段BC的长;
(2)当0≤y≤3时,请直接写出x的范围;
(3)点P是抛物线上位于第一象限的一个动点,连接CP,当∠BCP=90o时,求点P的坐标.
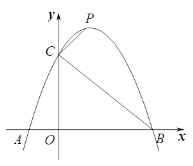
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行20分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是___________海里.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣![]() x2+bx+c的对称轴为直线x=﹣
x2+bx+c的对称轴为直线x=﹣![]() ,与x轴交于点A和点B(1,0),与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
,与x轴交于点A和点B(1,0),与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
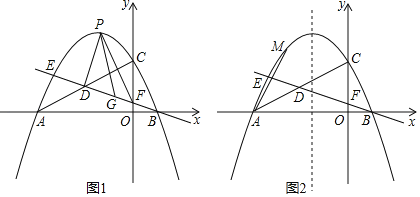
(1)求抛物线的解析式;
(2)点P是直线BE上方抛物线上一动点,连接PD、PF,当△PDF的面积最大时,在线段BE上找一点G,使得PG﹣![]() EG的值最小,求出PG﹣
EG的值最小,求出PG﹣![]() EG的最小值.
EG的最小值.
(3)如图2,点M为抛物线上一点,点N在抛物线的对称轴上,点K为平面内一点,当以A、M、N、K为顶点的四边形是正方形时,请求出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数
,1)在反比例函数![]() 的图象上.
的图象上.

(1)求反比例函数![]() 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP=![]() S△AOB,求点P的坐标;
S△AOB,求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
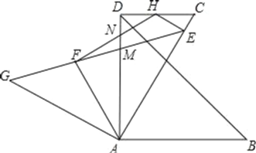
【题目】如图,将等腰Rt△GAE绕点A顺时针旋转60°得到△DAB,其中∠GAE=∠DAB=90°,GE与AD交于点M,过点D作DC∥AB交AE于点C.已知AF平分∠GAM,EH⊥AE交DC于点H,连接FH交DM于点N,若AC=2![]() ,则MN的值为______.
,则MN的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
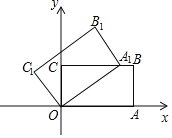
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为( )
A. (﹣![]() ) B. (﹣
) B. (﹣![]() ) C. (﹣
) C. (﹣![]() ) D. (﹣
) D. (﹣![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com