
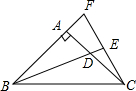
 如图,把Rt△ABD绕点A逆时针旋转90°至△ACF的位置,BD的延长线交CF于点E,连接BC,若∠FBE=∠CBE,试确定CE与BD的关系.
如图,把Rt△ABD绕点A逆时针旋转90°至△ACF的位置,BD的延长线交CF于点E,连接BC,若∠FBE=∠CBE,试确定CE与BD的关系. 分析 由旋转的性质得出△ACF≌△ABD,得出CF=BD,∠ACF=∠ABD,由直角三角形的性质和对顶角相等得出∠ACF+∠CDE=90°,因此∠CED=90°,CE⊥BD,由ASA证明△BCE≌△BFE,得出对应边相等BC=BF,由等腰三角形的三线合一性质得出CE=FE=$\frac{1}{2}$CF,即可得出结论.
解答 解:CE⊥BD,CE=$\frac{1}{2}$BD;理由如下:
由旋转的性质得:△ACF≌△ABD,
∴CF=BD,∠ACF=∠ABD,
∵∠BAD=90°,
∴∠ABD+∠ADB=90°,
∵∠CDE=∠ADB,
∴∠ACF+∠CDE=90°,
∴∠CED=90°,
∴CE⊥BD,
即CE⊥BD,
在△BCE和△BFE中,$\left\{\begin{array}{l}{∠CBE=∠FBE}&{\;}\\{BE=BE}&{\;}\\{∠BEC=∠BEF=90°}&{\;}\end{array}\right.$,
∴△BCE≌△BFE(ASA),
∴BC=BF,
∴CE=FE=$\frac{1}{2}$CF,
∴CE=$\frac{1}{2}$BD.
点评 本题考查了全等三角形的判定与性质、旋转的性质、直角三角形的性质、等腰三角形的判定与性质;熟练掌握旋转的性质,证明三角形全等是解决问题的关键.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
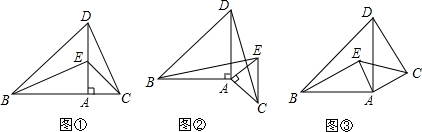
 已知△ABC中,AC=BC,∠ACB=90°,D,E分别为AB,BC上一点,连接DE.
已知△ABC中,AC=BC,∠ACB=90°,D,E分别为AB,BC上一点,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
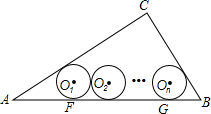 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,其中⊙O1,⊙O2,…⊙On,为n个(n≥2)相等的圆,⊙O1与⊙O2相外切,⊙O2与⊙O3相外切…,⊙On-1与⊙On相外切,⊙O1,⊙O2,…,⊙On都与AB相切,且⊙O1与AC相切,⊙On与BC相切,求这些等圆的半径r(用n表示).
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,其中⊙O1,⊙O2,…⊙On,为n个(n≥2)相等的圆,⊙O1与⊙O2相外切,⊙O2与⊙O3相外切…,⊙On-1与⊙On相外切,⊙O1,⊙O2,…,⊙On都与AB相切,且⊙O1与AC相切,⊙On与BC相切,求这些等圆的半径r(用n表示).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
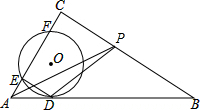 如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为12,弧DE的长为4π,AF=CE,P是边BC上的动点,连结AP、DP,则AP+DP的最小值是24$\sqrt{7}$.
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为12,弧DE的长为4π,AF=CE,P是边BC上的动点,连结AP、DP,则AP+DP的最小值是24$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
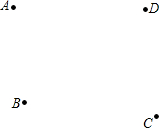 如图,已知A,B,C,D四个点.
如图,已知A,B,C,D四个点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com