
【题目】在平面直角坐标系中,△ABC的顶点坐标是A(﹣7,1),B(1,1),C(1,7).线段DE的端点坐标是D(7,﹣1),E(﹣1,﹣7).
(1)试说明如何平移线段AC,使其与线段ED重合;
(2)将△ABC绕坐标原点O逆时针旋转,使AC的对应边为DE,请直接写出点B的对应点F的坐标;
(3)画出(2)中的△DEF,并和△ABC同时绕坐标原点O逆时针旋转90°,画出旋转后的图形.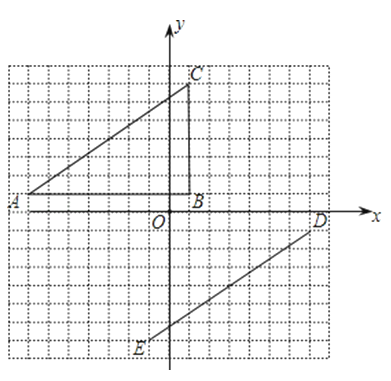
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】完成下面的证明
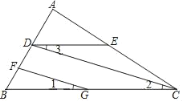
(1)如图,FG∥CD,∠1=∠3,∠B=50°,求∠BDE的度数.
解:∵FG∥CD(已知)
∴∠2=
又∵∠1=∠3,
∴∠3=∠2(等量代换)
∴BC∥
∴∠B+ =180°
又∵∠B=50°
∴∠BDE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学实验室:

制作4张全等的直角三角形纸片(如图1),把这4张纸片拼成以弦长c为边长的正方形构成“弦图”(如图2),古代数学家利用“弦图”验证了勾股定理.
探索研究:
(1)小明将“弦图”中的2个三角形进行了运动变换,得到图3,请利用图3证明勾股定理;
数学思考:
(2)小芳认为用其它的方法改变“弦图”中某些三角形的位置,也可以证明勾股定理.请你想一种方法支持她的观点(先在备用图中补全图形,再予以证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直径为1的圆从原点沿数轴向左滚动一周,圆上与原点重合的点O到达O′,设点O′表示的数为a.
(1)求a的值;
(2)求﹣(a﹣![]() )﹣π的算术平方根.
)﹣π的算术平方根.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角板如图甲放置,其中 ![]() ,
, ![]() ,斜边AB=6cm,DC=7cm把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点O,与D1E1相交于点F .
,斜边AB=6cm,DC=7cm把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点O,与D1E1相交于点F . 
(1)求 ![]() 的度数;
的度数;
(2)求线段AD1的长;
(3)若把三角形D1CE1绕着点 C 顺时针再旋转30°得△D2CE2 , 这时点B在△D2CE2的内部、外部、还是边上?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,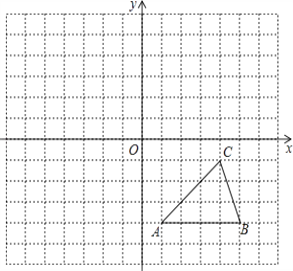
(1)写出A、B、C的坐标.
(2)以原点O为中心,将△ABC围绕原点O逆时针旋转180°得到△A1B1C1 , 画出△A1B1C1 .
(3)求(2)中C到C1经过的路径以及OB扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com