
【题目】已知:![]() 为
为![]() 的直径,
的直径,![]() ,
,![]() 为
为![]() 上一动点(不与
上一动点(不与![]() 、
、![]() 重合).
重合).

(1)如图1,若![]() 平分
平分![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .①求证:
.①求证:![]() ;②若
;②若![]() ,求
,求![]() 的长;
的长;
(2)如图2,若![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,连接
,连接![]() .求证:
.求证:![]() 为
为![]() 的切线.
的切线.
【答案】(1)①见解析,②2;(2)见解析
【解析】
(1)①先根据圆周角定理得出![]() ,再得出
,再得出![]() ,再根据角平分线的定义得出
,再根据角平分线的定义得出![]() ,最后根据三角形外角定理即可求证;②取
,最后根据三角形外角定理即可求证;②取![]() 中点
中点![]() ,连接
,连接![]() ,可得
,可得![]() 是中位线,根据平行线的性质得
是中位线,根据平行线的性质得![]() ,然后根据等腰三角形的性质得出
,然后根据等腰三角形的性质得出![]() ,最后再根据中位线的性质得出
,最后再根据中位线的性质得出![]() ;
;
(2)![]() 上截取
上截取![]() ,连接
,连接![]() ,由题意先得出
,由题意先得出![]() ,再得出
,再得出![]() ,然后由旋转性质得
,然后由旋转性质得![]() 、
、![]() ,再根据同角的补角相等得出
,再根据同角的补角相等得出![]() ,然后证的
,然后证的![]() ,最后得出
,最后得出![]() 即可证明.
即可证明.
解:(1)①证明:![]() 为
为![]() 的直径,
的直径,
![]() .
.
![]() ,
,
![]() ,
,![]() .
.
![]() .
.
![]() 平分
平分![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ;
;
②解法一:如图,取![]() 中点
中点![]() ,连接
,连接![]() ,
,
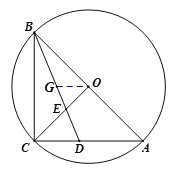
![]() 为
为![]() 的中点,
的中点,
![]() ,
,![]() .
.
![]() .
.
![]() ,
,![]() ,
,
![]() .
.
![]() .
.
![]() ;
;
解法二:如图,作![]() ,垂足为
,垂足为![]() ,
,
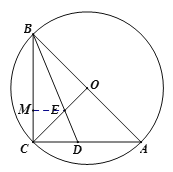
![]() 平分
平分![]() ,
,![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
在![]() 中,
中,![]() .
.
![]() ;
;
解法三:如图,作![]() ,垂足为
,垂足为![]() ,
,
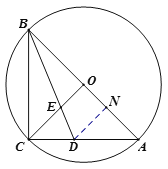
设![]()
![]() 平分
平分![]() ,
,![]() ,
,
![]() .
.
![]()
∴![]()
∴![]() ,即
,即![]()
∴![]()
解得:![]()
∴![]()
(2)证明(法一):如图,在![]() 上截取
上截取![]() ,连接
,连接![]() .
.
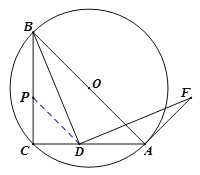
![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() .
.
由旋转性质得,![]() ,
,![]() .
.
![]()
![]() ,
,
![]() .
.
![]() .(
.(![]() 没写不扣分)
没写不扣分)
![]() .
.
![]() .
.
![]() .
.
![]() 为
为![]() 的切线.
的切线.
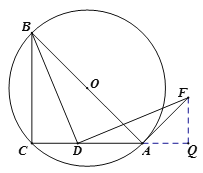
证法二:如图,延长![]() 到
到![]() ,使
,使![]() .
.
由旋转性质得,![]() ,
,![]() .
.
![]() .
.
![]() ,
,
![]() .
.
![]() .(
.(![]() 没写不扣分)
没写不扣分)
![]() ,
,![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() 为
为![]() 的切线.
的切线.
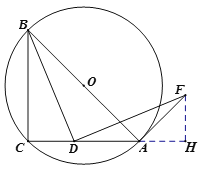
证法三:作![]() 交
交![]() 延长线于点
延长线于点![]() .(余下略)
.(余下略)
由旋转性质得,![]() ,
,![]()
∴![]()
![]() ,
,
∴![]() .
.
∵![]()
∴![]()
∴![]() 、
、![]()
![]()
∴![]()
∴![]()
∴![]()
∴![]()
∵![]() 为
为![]() 的直径,
的直径,
∴![]()
∴![]()
∴![]()
∴![]() .
.
∴![]() 为
为![]() 的切线.
的切线.


科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为![]() 个单位的正方形,在建立平面直角坐标系后,
个单位的正方形,在建立平面直角坐标系后,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 的坐标为
的坐标为![]() .
.

![]() 以点
以点![]() 为位似中心,在
为位似中心,在![]() 轴的左侧将
轴的左侧将![]() 放大得到
放大得到![]() ,使得
,使得![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍,在网格中画出图形,并直接写出点
倍,在网格中画出图形,并直接写出点![]() 所对应的点
所对应的点![]() 的坐标.
的坐标.
![]() 在网格中,画出
在网格中,画出![]() 绕原点
绕原点![]() 顺时针旋转
顺时针旋转![]() 的
的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
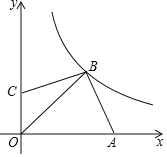
【题目】如图所示平面直角坐标系中,点A,C分别在x轴和y轴上,点B在第一象限,BC=BA,∠ABC=90°,反比例函数y=![]() .(x>0)的图象经过点B,若OB=2
.(x>0)的图象经过点B,若OB=2![]() ,则k的值为_____.
,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的过长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD、BC交于点F、E,连接AE.
(1)求证:AQ⊥DP;
(2)求证:AO2=ODOP;
(3)当BP=1时,求QO的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在东西方向的海岸线l上有长为300米的码头AB,在码头的最西端A处测得轮船M在它的北偏东45°方向上;同一时刻,在A点正东方向距离100米的C处测得轮船M在北偏东22°方向上.
(1)求轮船M到海岸线l的距离;(结果精确到0.01米)
(2)如果轮船M沿着南偏东30°的方向航行,那么该轮船能否行至码头AB靠岸?请说明理由.
(参考数据:sin22°≈0.375,cos22°≈0.927,tan22°≈0.404,![]() ≈1.732.)
≈1.732.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践—探究正方形旋转中的数学问题
问题情境:已知正方形![]() 中,点
中,点![]() 在
在![]() 边上,且
边上,且![]() .将正方形
.将正方形![]() 绕点
绕点![]() 顺时针旋转得到正方形
顺时针旋转得到正方形![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 分别是点
分别是点![]() ,
,![]() ,
,![]() ,
,![]() 的对应点).同学们通过小组合作,提出下列数学问题,请你解答.
的对应点).同学们通过小组合作,提出下列数学问题,请你解答.
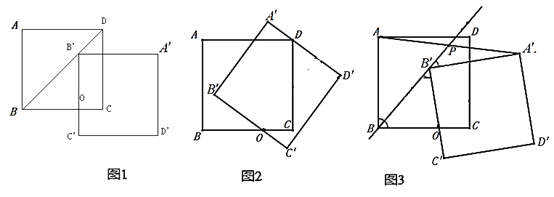
特例分析:(1)“乐思”小组提出问题:如图1,当点![]() 落在正方形
落在正方形![]() 的对角线
的对角线![]() 上时,设线段
上时,设线段![]() 与
与![]() 交于点
交于点![]() .求证:四边形
.求证:四边形![]() 是矩形;
是矩形;
(2)“善学”小组提出问题:如图2,当线段![]() 经过点
经过点![]() 时,猜想线段
时,猜想线段![]() 与
与![]() 满足的数量关系,并说明理由;
满足的数量关系,并说明理由;
深入探究:(3)请从下面![]() ,
,![]() 两题中任选一题作答.我选择题.
两题中任选一题作答.我选择题.
A.在图2中连接![]() 和
和![]() ,请直接写出
,请直接写出![]() 的值.
的值.
B.“好问”小组提出问题:如图3,在正方形![]() 绕点
绕点![]() 顺时针旋转的过程中,设直线
顺时针旋转的过程中,设直线![]() 交线段
交线段![]() 于点
于点![]() .连接
.连接![]() ,并过点
,并过点![]() 作
作![]() 于点
于点![]() .请在图3中补全图形,并直接写出
.请在图3中补全图形,并直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光污染是继废气、废水、废渣和噪声等污染之后的一种新的环境污染源,主要包括白亮污染、人工白昼污染和彩光污染,如图,小明家正对面的高楼外墙上安装着一幅巨型广告宣传牌AB,小明想要测量窗外的广告宣传牌AB的高度,他发现晚上家里熄灯后对面楼上的广告宣传牌从A处发出的光恰好从窗户的最高点C处射进房间落在地板上F处,从窗户的最低点D处射进房间向落在地板上E处(B、O、E、F在同一直线E),小明测得窗户距地面的高度OD=1m,窗高CD=1.5m,并测得OE=1m,OF=3m.请根据以上测量数据,求广告宣传牌AB的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中
(1)请你利用无刻度的直尺和圆规在平面内画出满足PB2+PC2=BC2的所有点P构成的图形,并在所作图形上用尺规确定到边AC、BC距离相等的点P.(作图必须保留作图痕迹)
(2)在(1)的条件下,连接BP,若BC=15,AC=14,AB=13,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 的顶点为
的顶点为![]() ,且经过点
,且经过点![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
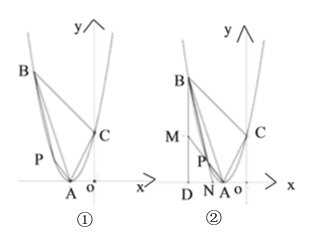
(1)求抛物线对应的函数表达式;
(2)点![]() 为该抛物线上点
为该抛物线上点![]() 与点
与点![]() 之间的一动点.
之间的一动点.
①若![]() ,求点
,求点![]() 的坐标.
的坐标.
②如图②,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,连接
,连接![]() 延长交
延长交![]() 于点
于点![]() .试说明
.试说明![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com