
【题目】如图,在平面直角坐标系中,抛物线![]() 的顶点为
的顶点为![]() ,且经过点
,且经过点![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
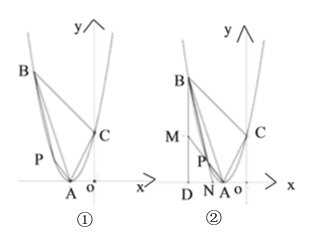
(1)求抛物线对应的函数表达式;
(2)点![]() 为该抛物线上点
为该抛物线上点![]() 与点
与点![]() 之间的一动点.
之间的一动点.
①若![]() ,求点
,求点![]() 的坐标.
的坐标.
②如图②,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,连接
,连接![]() 延长交
延长交![]() 于点
于点![]() .试说明
.试说明![]() 为定值.
为定值.
【答案】(1)![]() ;(2)①点
;(2)①点![]() 的坐标为
的坐标为![]() ,
,![]() ;②
;②![]() ,是定值.
,是定值.
【解析】
(1)设函数为![]() ,把
,把![]() 代入即可求解;
代入即可求解;
(2)①先求出直线AB解析式,求出C’点,得到![]() ,再求出
,再求出![]() ,设点
,设点![]() ,过
,过![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,得到
,得到![]() ,根据三角形面积公式得
,根据三角形面积公式得![]() ,解出x即可求解;
,解出x即可求解;
②过![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,设
,设![]() ,表示出
,表示出![]() ,故
,故![]() ,根据
,根据![]() ,得
,得![]() ,故
,故![]() ,即
,即![]() ,得到
,得到![]() .再过
.再过![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,根据 相似三角形的性质得到
,根据 相似三角形的性质得到![]() ,可得
,可得![]() 的值即为定值.
的值即为定值.
(1)解:设![]() ,把点
,把点![]() 代入,
代入,
得![]() ,解得
,解得![]() ,
,
∴该抛物线对应的函数表达式为![]() .
.
(2)①设直线![]() 的函数表达式为
的函数表达式为![]() ,
,
把![]() ,
,![]() 代入,得
代入,得![]() ,解得
,解得![]() .
.
∴直线![]() 的函数表达式为
的函数表达式为![]() .
.
设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,则点
,则点![]() ,∴
,∴![]() .
.
![]() ,
,![]() .
.
设点![]() ,过
,过![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,则
,则![]() ,
,
∴![]() ,
,
![]() ,
,![]() ,
,
所以点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
②过![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,
,![]() ,即
,即![]() ,故
,故![]() .
.
过![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,
,
由![]() ,得
,得![]() ,
,![]() ,即
,即![]() ,故
,故![]() .
.
所以![]() ,是定值.
,是定值.
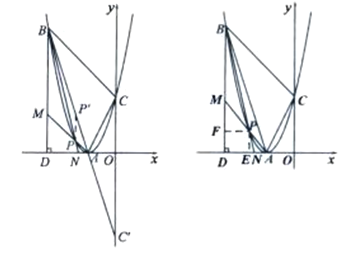


科目:初中数学 来源: 题型:
【题目】已知:![]() 为
为![]() 的直径,
的直径,![]() ,
,![]() 为
为![]() 上一动点(不与
上一动点(不与![]() 、
、![]() 重合).
重合).

(1)如图1,若![]() 平分
平分![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .①求证:
.①求证:![]() ;②若
;②若![]() ,求
,求![]() 的长;
的长;
(2)如图2,若![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,连接
,连接![]() .求证:
.求证:![]() 为
为![]() 的切线.
的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
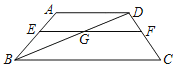
【题目】如图,在梯形ABCD中,点E,F分别在边AB,CD上,AD∥EF∥BC,EF与BD交于点G,AD=5,BC=10,![]() =
=![]() .
.
(1)求EF的长;
(2)设![]() =
=![]() ,
,![]() =
=![]() ,那么
,那么![]() = ,
= ,![]() = .(用向量
= .(用向量![]() 、
、![]() 表示)
表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行
销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)于销售单价x(元
/个)之间的对应关系如图所示.
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查销售规律,求利润w(元)与销售单价x(元/个)之间的
函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试求此时这种许愿瓶的销售单价,并求出
最大利润.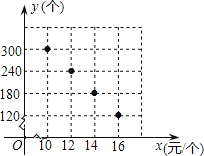
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
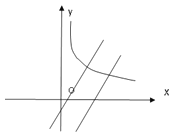
【题目】平面直角坐标系中,函数![]() (x>0),y=x-1,y=x-4的图象如图所示,p(a , b)是直线
(x>0),y=x-1,y=x-4的图象如图所示,p(a , b)是直线![]() 上一动点,且在第一象限.过P作PM∥x轴交直线
上一动点,且在第一象限.过P作PM∥x轴交直线![]() 于M,过P作PN∥y轴交曲线
于M,过P作PN∥y轴交曲线![]() 于N.
于N.
(1)当PM=PN时,求P点坐标
(2)当PM > PN时,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦放假期间,小明和小华准备到西安的大雁塔(记为A)、白鹿原(记为B)、兴庆公园(记为C)、秦岭国家植物园(记为D)中的一个景点去游玩,他们各自在这四个景点中任选一个,每个景点被选中的可能性相同.
(1)求小明选择去白鹿原游玩的概率;
(2)用树状图或列表的方法求小明和小华都选择去秦岭国家植物园游玩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把函数C1:y=ax2﹣2ax﹣3a(a≠0)的图象绕点P(m,0)旋转180°,得到新函数C2的图象,我们称C2是C1关于点P的相关函数.C2的图象的对称轴与x轴交点坐标为(t,0).
(1)填空:t的值为 (用含m的代数式表示)
(2)若a=﹣1,当![]() ≤x≤t时,函数C1的最大值为y1,最小值为y2,且y1﹣y2=1,求C2的解析式;
≤x≤t时,函数C1的最大值为y1,最小值为y2,且y1﹣y2=1,求C2的解析式;
(3)当m=0时,C2的图象与x轴相交于A,B两点(点A在点B的右侧).与y轴相交于点D.把线段AD原点O逆时针旋转90°,得到它的对应线段A′D′,若线A′D′与C2的图象有公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com