

| 排量(L) | 小于1.6 | 1.6 | 1.8 | 大于1.8 |
| 轿车数量(辆) | 60 | 200 | 80 | 60 |
分析 (1)设2013年该市私人轿车拥有量为x万辆,根据2014年拥有量=2013年拥有量×(1+2014年的增长率)列出方程,解方程可得;
(2)设2012年增长率为m,根据2011年拥有量×(1+增长率)=2012年拥有量,列方程求解即可;
(3)根据2014年20私人轿车总量由14年1.6L的私人轿车占私人轿车拥有量的比例可得排量为1.6L的私人轿车数,再计算碳排放总量.
解答 解:(1)设2013年该市私人轿车拥有量为x万辆,根据题意,
得:(1+30%)x=108,解得:x=83,
答:2013年该市私人轿车拥有量约是83万辆;
(2)设2012年增长率为m,则60(1+m)=69,
解得:m=0.15=15%,补全统计图如下图所示: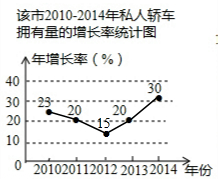
(3)2014年1.6L私人轿车的拥有量为:108×(200÷400)=54(万辆),
所以2014年该市仅排量为1.6L的私人轿车的碳排放总量为:540000×2.7=1458000(万吨),
答:2014年该市仅排量为1.6L的私人轿车的碳排放总量为1458000万吨.
点评 本题考查的是条形统计图和折线统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据,折线统计图表示的是事物的变化情况.


科目:初中数学 来源: 题型:选择题
| A. | 6cm、5cm、10cm | B. | 5cm、4cm、9cm | C. | 4cm、6cm、9cm | D. | 2cm、3cm、4cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=7,b=24,c=25 | B. | a=11,b=60,c=61 | C. | a=$\frac{8}{3}$,b=2,c=$\frac{13}{3}$ | D. | a=1,b=$\frac{5}{4}$,c=$\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 商品A的数量 | 商品B的数量 | 商品C的数量 | 总费用(元) | |
| 第一次 | 5 | 4 | 3 | 390 |
| 第二次 | 5 | 4 | 5 | 312 |
| 第三次 | 0 | 6 | 4 | 420 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在菱形ABCD中,对角线AC=10,BD=24,
如图,在菱形ABCD中,对角线AC=10,BD=24,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com