
分析 已知等式左边分子分母变形,将a2+4a+1=0整理后代入求出m的值即可.
解答 解:∵a2+4a+1=0,
∴a2=-4a-1,-4a=a2+1,
分子=a4+a2m+1=(-4a-1)2+1+a2m=16a2+8a+1+1+a2m=16a2+2(4a+1)+a2m=14a2+a2m=(14+m)a2,
分母=3a(-4a-1)+a2m+3a=-12a2+a2m=a2(m-12),
∴$\frac{{a}^{2}(14+m)}{{a}^{2}(m-12)}$=5,即14+m=5(m-12),
解得:m=$\frac{37}{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题

| 排量(L) | 小于1.6 | 1.6 | 1.8 | 大于1.8 |
| 轿车数量(辆) | 60 | 200 | 80 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
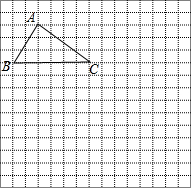 △ABC在网格中的位置如图所示,请根据下列要求作图:
△ABC在网格中的位置如图所示,请根据下列要求作图:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
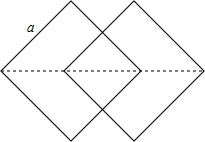 如图,这是由一个边长为a的正方形沿一条对角线的方向平移$\frac{\sqrt{2}a}{2}$得到的图案.
如图,这是由一个边长为a的正方形沿一条对角线的方向平移$\frac{\sqrt{2}a}{2}$得到的图案.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(-1,0),另一个交点为B,且与y轴交于点C.
如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(-1,0),另一个交点为B,且与y轴交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com