
分析 (1)设出2008年第一季度企业销售总收入为x万元,根据补贴=销售收入×补贴比例×省级财政负担比例得出关于x的一元一次方程,解方程即可得出结论;
(2)设出2008年第一季度家电下乡产品销售总量为y万台,根据各家店销售比例和销售价格得出关于y的一元一次方程,解方程即可得出结论;
(3)设2009年第一季度洗衣机价格下降百分比为m,用含m的代数式表示出各家店销售数量和销售价格,结合已知得出关于m的一元二次方程,解出方程即可得出2009年第一季度企业的销售总收入增长的百分数,结合2008年第一季度的销售总收入即可得出结论.
解答 解:(1)设2008年第一季度企业销售总收入为x万元,根据题意可得:
13%•x•20%=5.46,解得:x=210.
答:2008年第一季度企业销售总收入为210万元.
(2)设2008年第一季度家电下乡产品销售总量为y万台,则销售彩电$\frac{1}{2}$y万台,销售冰箱$\frac{1}{3}$y万台,销售洗衣机$\frac{1}{6}$y万台,
根据题意可得:2500×$\frac{1}{2}$y+2200×$\frac{1}{3}$y+2100×$\frac{1}{6}$y=210,
解得:y=0.09.
答:2008年第一季度家电下乡产品销售总量为0.09万台.
(3)设2009年第一季度洗衣机价格下降百分比为m,则彩电、冰箱价格下降百分比为2m,
故2009年第一季度彩电价格为2500(1-2m)元;冰箱价格为2200(1-2m)元;洗衣机价格为2100(1-m)元,
则2009年第一季度彩电销售增加百分数为4m,冰箱销售量增加百分数为4m,洗衣机销售量增加百分数为2m,
由(2)可知2008年第一季度下乡彩电销售量为900÷2=450台,冰箱为900÷3=300台,洗衣机为900÷6=150台,
∴2009年第一季度彩电销售量为450(1+4m)台,冰箱为300(1+4m)台,洗衣机为150(1+2m),
∴2009年第一季度销售总收入为2500(1-2m)×450(1+4m)+2200(1-2m)×300(1+4m)+2100(1-m)×150(1+2m)=2100000+3885000m-14910000m2,
依题意有($\frac{2100000+3885000m-14910000{m}^{2}}{2100000}$-1)×100%=2m,
解得:m=0(舍去),m≈0.026%.
∴2009年第一季度销售总收入=2100000+2100000×2×0.026%≈220.92(万元),
∴2009年第一季度农民获得的补贴=220.92×13%≈28.72(万元).
答:2009年第一季度农民购买家电获得的补贴约为28.72万元.
点评 本题考查了一元二次方程的应用与解一元一次方程,解题的关键是:(1)列出关于2008年第一季度企业销售总收入的一元一次方程;(2)列出关于2008年第一季度家电下乡产品销售总量的一元一次方程;(3)找出关于2009年第一季度洗衣机价格下降百分比的一元二次方程.本题属于中档题,(1)(2)比较简单,(3)数据太大,运算繁琐,在运算过程中要格外细心.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:选择题
| A. | a=7,b=24,c=25 | B. | a=11,b=60,c=61 | C. | a=$\frac{8}{3}$,b=2,c=$\frac{13}{3}$ | D. | a=1,b=$\frac{5}{4}$,c=$\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在菱形ABCD中,对角线AC=10,BD=24,
如图,在菱形ABCD中,对角线AC=10,BD=24,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
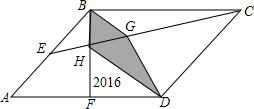 如图,平行四边形ABCD中,E、F分别为AB、AD的中点,连接BF、CE交于点H,连接HD,过B点作BG平行HD,已知△HFD的面积是2016平方厘米,求阴影四边形BGDH的面积?
如图,平行四边形ABCD中,E、F分别为AB、AD的中点,连接BF、CE交于点H,连接HD,过B点作BG平行HD,已知△HFD的面积是2016平方厘米,求阴影四边形BGDH的面积?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,AB=4,BC=8,∠B=60°,点P以每秒2个单位速度,从点B出发沿射线BA方向运动,同时直线l以每秒1个单位速度,从CD出发沿射线CB方向运动,分别交BC,AC于点G,H,连结PG,设运动的时间为t,当G与B重合时,运动停止.
如图,在?ABCD中,AB=4,BC=8,∠B=60°,点P以每秒2个单位速度,从点B出发沿射线BA方向运动,同时直线l以每秒1个单位速度,从CD出发沿射线CB方向运动,分别交BC,AC于点G,H,连结PG,设运动的时间为t,当G与B重合时,运动停止.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
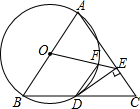 如图.△ABC中,AB=AC,以AB为直径的⊙O交BC于D点,DE⊥AC于点E.
如图.△ABC中,AB=AC,以AB为直径的⊙O交BC于D点,DE⊥AC于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com