
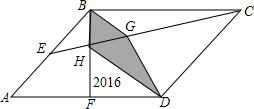
 如图,平行四边形ABCD中,E、F分别为AB、AD的中点,连接BF、CE交于点H,连接HD,过B点作BG平行HD,已知△HFD的面积是2016平方厘米,求阴影四边形BGDH的面积?
如图,平行四边形ABCD中,E、F分别为AB、AD的中点,连接BF、CE交于点H,连接HD,过B点作BG平行HD,已知△HFD的面积是2016平方厘米,求阴影四边形BGDH的面积? 分析 如延长FE交CB的延长线于M,连接BD交CE于N,先证明$\frac{BH}{BF}=\frac{BN}{EF}=\frac{BN}{EF}=\frac{CB}{CM}=\frac{2}{3}$,求出△BHD面积,再证明△BEG∽△DCH,得BG:HD=EB:CD=1:2,得到S△BGH:S△HDG=1:2,由此可以解决问题.
解答 解:如图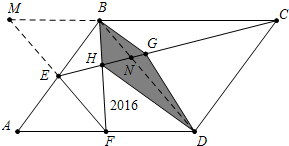 延长FE交CB的延长线于M,连接BD交CE于N.
延长FE交CB的延长线于M,连接BD交CE于N.
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AB∥CD,AD∥BC,
∴∠M=∠AFE,
在△MEB和△FEA中,
$\left\{\begin{array}{l}{∠M=∠AFE}\\{BE=AE}\\{∠MEB=∠AEF}\end{array}\right.$,
∴△MEB≌△FEA,
∴BM=AM,ME=EF,
∵AF=FD,AE=EB,
∴EF∥BD,
∴$\frac{BN}{EF}=\frac{BH}{FH}=\frac{BN}{MF}=\frac{CB}{CM}=\frac{2}{3}$,
∴${S}_{△BHD}=\frac{2}{3}$×2016=1344,
∵BG∥HD,
∴∠BGE=∠CHD,S△BHD=S△HDG,
∵∠BEG=∠DCH,
∴△BEG∽△DCH,
∴BG:HD=EB:CD=1:2,
∴S△BGH:S△HDG=1:2,
∴S△BHG=672,
∴S阴=S△BHG+S△HGD=672+1344=2016.
点评 本题考查平行四边形的性质、全等三角形的判定和性质、相似三角形的判定和性质,解题的关键是添加辅助线求出相应线段的比,题目比较难,综合性强.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 一、二、三 | B. | 一、三、四 | C. | 二、三、四, | D. | 一、二、四 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
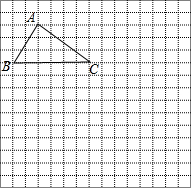 △ABC在网格中的位置如图所示,请根据下列要求作图:
△ABC在网格中的位置如图所示,请根据下列要求作图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
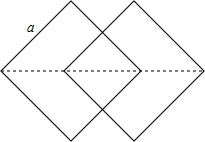 如图,这是由一个边长为a的正方形沿一条对角线的方向平移$\frac{\sqrt{2}a}{2}$得到的图案.
如图,这是由一个边长为a的正方形沿一条对角线的方向平移$\frac{\sqrt{2}a}{2}$得到的图案.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com