
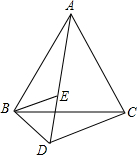
 如图,已知△ABC和△BED都是等边三角形,且A、E、D在一条直线上,且DC=4,BD=2,求AD的长度?
如图,已知△ABC和△BED都是等边三角形,且A、E、D在一条直线上,且DC=4,BD=2,求AD的长度? 分析 根据等边三角形的性质得出AB=BC,BE=BD,∠ABC=∠EBD=60°,求出∠ABE=∠CBD,根据SAS推出△ABE≌△CBD,根据全等得出AE=CD=4,即可求出答案.
解答 解:∵△ABC和△BED都是等边三角形,
∴AB=BC,BE=BD,∠ABC=∠EBD=60°,
∴∠ABE=∠CBD=60°-∠CBE,
在△ABE和△CBD中
$\left\{\begin{array}{l}{BA=BC}\\{∠ABE=∠CBD}\\{BE=BD}\end{array}\right.$
∴△ABE≌△CBD(SAS),
∴AE=CD=4,
∵△BED是等边三角形,
∴DE=BD=2,
∴AD=2+4=6.
点评 本题考查了全等三角形的性质和判定,等边三角形的性质的应用,能推出△ABE≌△CBD是解此题的关键.


科目:初中数学 来源: 题型:填空题
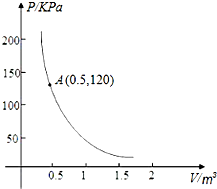 某校举行田径运动会,学校准备了某种气球,这些气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内的气压大于150KPa时,气球会将爆炸,为了安全起见,气体的体积应不小于0.4m3.
某校举行田径运动会,学校准备了某种气球,这些气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内的气压大于150KPa时,气球会将爆炸,为了安全起见,气体的体积应不小于0.4m3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线.以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点,则抛物线的解析式是y=-$\frac{1}{9}$x2+$\frac{4}{3}$x.
如图所示的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线.以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点,则抛物线的解析式是y=-$\frac{1}{9}$x2+$\frac{4}{3}$x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com