
ЁОЬтФПЁПЕБЭМаЮОпгаСкБпЯрЕШЕФЬиеїЪБЃЌЮвУЧПЩвдАбЭМаЮЕФвЛВПЗжШЦзХЙЋЙВЖЫЕуа§зЊЃЌетбљНЋЗжЩЂЕФЬѕМўМЏжаЦ№РДЃЌДгЖјДяЕННтОіЮЪЬтЕФФПЕФ
![]() ШчЭМ1ЃЌЕШбќжБНЧШ§НЧаЮ
ШчЭМ1ЃЌЕШбќжБНЧШ§НЧаЮ![]() ФкгавЛЕу
ФкгавЛЕу![]() СЌНг
СЌНг![]() ЮЊЬНОП
ЮЊЬНОП![]() Ш§ЬѕЯпЖЮМфЕФЪ§СПЙиЯЕЃЌЮвУЧПЩвдНЋ
Ш§ЬѕЯпЖЮМфЕФЪ§СПЙиЯЕЃЌЮвУЧПЩвдНЋ![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЕУЕН
ЕУЕН![]() СЌНг
СЌНг![]() дђ
дђ![]() ___ ____
___ ____![]() ЪЧ_ Ш§НЧаЮЃЌ
ЪЧ_ Ш§НЧаЮЃЌ![]() Ш§ЬѕЯпЖЮЕФЪ§СПЙиЯЕЪЧ_ ЃЛ
Ш§ЬѕЯпЖЮЕФЪ§СПЙиЯЕЪЧ_ ЃЛ
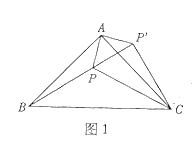
![]() ШчЭМ2ЃЌЕШБпШ§НЧаЮ
ШчЭМ2ЃЌЕШБпШ§НЧаЮ![]() ФквЛЕуPЃЌСЌНг
ФквЛЕуPЃЌСЌНг![]() ЧыНшжњЕквЛЮЪЕФЗНЗЈЬНОП
ЧыНшжњЕквЛЮЪЕФЗНЗЈЬНОП![]() Ш§ЬѕЯпЖЮМфЕФЪ§СПЙиЯЕЃЎ
Ш§ЬѕЯпЖЮМфЕФЪ§СПЙиЯЕЃЎ
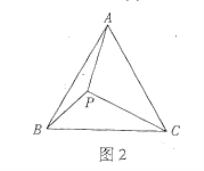
![]() ШчЭМ3 ЃЌдкЫФБпаЮ
ШчЭМ3 ЃЌдкЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() Еу
Еу![]() дкЫФБпаЮФкВПЃЌЧв
дкЫФБпаЮФкВПЃЌЧв![]()
![]() ЧыжБНгаДГі
ЧыжБНгаДГі![]() ЕФГЄЃЎ
ЕФГЄЃЎ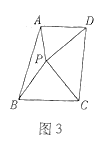
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌжБНЧЃЌ
ЃЌжБНЧЃЌ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЌжЄУїЯъМћНтЮіЃЛЃЈ3ЃЉ
ЃЌжЄУїЯъМћНтЮіЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОна§зЊЕФаджЪвзЕУ![]()
![]() ЃЌ
ЃЌ![]() ЪЧжБНЧШ§НЧаЮЃЌдйИљОнЙДЙЩЖЈРэМДПЩЧѓНт.
ЪЧжБНЧШ§НЧаЮЃЌдйИљОнЙДЙЩЖЈРэМДПЩЧѓНт.
ЃЈ2ЃЉНЋ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() ЕУ
ЕУ![]() СЌНг
СЌНг![]() ПЩЕУ
ПЩЕУ![]() ЮЊЕШБпШ§НЧаЮЃЌ
ЮЊЕШБпШ§НЧаЮЃЌ![]() ЃЌдйИљОн
ЃЌдйИљОн![]() РћгУЙДЙЩЖЈРэМДПЩЧѓНт.
РћгУЙДЙЩЖЈРэМДПЩЧѓНт.
ЃЈ3ЃЉНЋ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() жС
жС![]() СЌНг
СЌНг![]() дђ
дђ![]() ЃЌИљОн
ЃЌИљОн![]() ЃЌЕУЕН
ЃЌЕУЕН![]() ЃЌдйИљОн
ЃЌдйИљОн![]() ЃЌЕУЕН
ЃЌЕУЕН![]() МД
МД![]() ЃЌдк
ЃЌдк![]() жаПЩЧѓЕУ
жаПЩЧѓЕУ![]() ЃЌдйИљОн
ЃЌдйИљОн![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌДгЖјжЄУї
ЃЌДгЖјжЄУї![]() МДПЩЧѓНт.
МДПЩЧѓНт.
![]() Ёп
Ёп![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЕУЕН
ЕУЕН![]()
Ёр![]() ЃЌЁЯ
ЃЌЁЯ![]() =
=![]()
Ёр![]()
ЁпBPЁЭ![]()
Ёр![]() ЪЧжБНЧШ§НЧаЮЃЎ
ЪЧжБНЧШ§НЧаЮЃЎ
Ёр![]()
МД![]()
![]()
![]() ШчЭМЃЌНЋ
ШчЭМЃЌНЋ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() ЕУ
ЕУ![]() СЌНг
СЌНг![]()
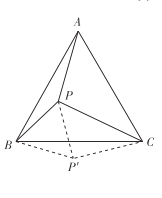
дђ![]() ЮЊЕШБпШ§НЧаЮЃЌ
ЮЊЕШБпШ§НЧаЮЃЌ
![]()
![]()
![]() ЃЎ
ЃЎ
![]() ЃЎНЋ
ЃЎНЋ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() жС
жС![]() СЌНг
СЌНг![]()
дђ![]() ЃЎ
ЃЎ
![]()
![]() ЃЎ
ЃЎ
![]() ЃЌ
ЃЌ
![]() МД
МД![]() ЃЎ
ЃЎ
дк![]() жаПЩЧѓЕУ
жаПЩЧѓЕУ![]() ЃЎ
ЃЎ
![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
ПЩжЄ![]()
дђ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
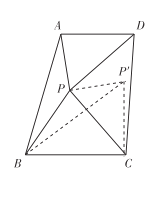
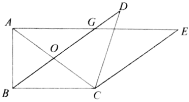
ЁОЬтФПЁПШчЭМ1ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЁЂ
ЁЂ![]() ЗжБ№дкБп
ЗжБ№дкБп![]() ЁЂ
ЁЂ![]() ЩЯЃЌ
ЩЯЃЌ![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЌЕу
ЃЌЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЗжБ№ЮЊ
ЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЕФжаЕуЃЎ
ЕФжаЕуЃЎ

ЃЈ1ЃЉЙлВьВТЯыЭМ1жаЃЌЯпЖЮ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЪЧ_______ЃЌЮЛжУЙиЯЕЪЧ_______ЃЛ
ЕФЪ§СПЙиЯЕЪЧ_______ЃЌЮЛжУЙиЯЕЪЧ_______ЃЛ
ЃЈ2ЃЉЬНОПжЄУїАб![]() ШЦЕу
ШЦЕу![]() ФцЪБеыЗНЯђа§зЊЕНЭМ2ЕФЮЛжУЃЌСЌНс
ФцЪБеыЗНЯђа§зЊЕНЭМ2ЕФЮЛжУЃЌСЌНс![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌХаЖЯ
ЃЌХаЖЯ![]() ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЭиеЙбгЩьАб![]() ШЦЕу
ШЦЕу![]() дкЦНУцФкздгЩа§зЊЃЌШє
дкЦНУцФкздгЩа§зЊЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЧыжБНгаДГі
ЃЌЧыжБНгаДГі![]() УцЛ§ЕФзюДѓжЕЃЎ
УцЛ§ЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
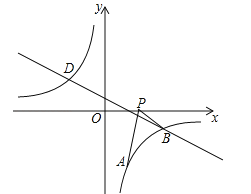
ЁОЬтФПЁПЃЈ2016КўББЪЁЛЦИдЪаЃЉШчЭМЃЌвбжЊЕуAЃЈ1ЃЌaЃЉЪЧЗДБШР§КЏЪ§![]() ЕФЭМЯѓЩЯвЛЕуЃЌжБЯп
ЕФЭМЯѓЩЯвЛЕуЃЌжБЯп![]() гыЗДБШР§КЏЪ§
гыЗДБШР§КЏЪ§![]() ЕФЭМЯѓдкЕкЫФЯѓЯоЕФНЛЕуЮЊЕуBЃЎ
ЕФЭМЯѓдкЕкЫФЯѓЯоЕФНЛЕуЮЊЕуBЃЎ
ЃЈ1ЃЉЧѓжБЯпABЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЖЏЕуPЃЈxЃЌ0ЃЉдкxжсЕФе§АыжсЩЯдЫЖЏЃЌЕБЯпЖЮPAгыЯпЖЮPBжЎВюДяЕНзюДѓЪБЃЌЧѓЕуPЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=xЉ4ЃЛЃЈ2ЃЉPЃЈ4ЃЌ0ЃЉЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЯШАбAЃЈ1ЃЌaЃЉДњШыЗДБШР§КЏЪ§НтЮіЪНЧѓГіaЕУЕНAЕузјБъЃЌдйНтЗНГЬзщ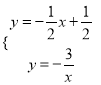 ЃЌЕУBЕузјБъЃЌШЛКѓРћгУД§ЖЈЯЕЪ§ЗЈЧѓABЕФНтЮіЪНЃЛ
ЃЌЕУBЕузјБъЃЌШЛКѓРћгУД§ЖЈЯЕЪ§ЗЈЧѓABЕФНтЮіЪНЃЛ
ЃЈ2ЃЉжБЯпABНЛxжсгкЕуQЃЌШчЭМЃЌРћгУxжсЩЯЕуЕФзјБъЬиеїЕУЕНQЕузјБъЃЌдђPAЉPBЁмABЃЈЕБPЁЂAЁЂBЙВЯпЪБШЁЕШКХЃЉЃЌгкЪЧПЩХаЖЯЕБPЕудЫЖЏЕНQЕуЪБЃЌЯпЖЮPAгыЯпЖЮPBжЎВюДяЕНзюДѓЃЌДгЖјЕУЕНPЕузјБъЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉАбAЃЈ1ЃЌaЃЉДњШы![]() ЕУa=Љ3ЃЌдђAЃЈ1ЃЌЉ3ЃЉЃЌНтЗНГЬзщЃК
ЕУa=Љ3ЃЌдђAЃЈ1ЃЌЉ3ЃЉЃЌНтЗНГЬзщЃК 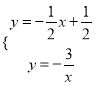 ЃЌЕУЃК
ЃЌЕУЃК ![]() Лђ
Лђ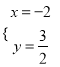 ЃЌдђBЃЈ3ЃЌЉ1ЃЉЃЌЩшжБЯпABЕФНтЮіЪНЮЊy=kx+bЃЌАбAЃЈ1ЃЌЉ3ЃЉЃЌBЃЈ3ЃЌЉ1ЃЉДњШыЕУЃК
ЃЌдђBЃЈ3ЃЌЉ1ЃЉЃЌЩшжБЯпABЕФНтЮіЪНЮЊy=kx+bЃЌАбAЃЈ1ЃЌЉ3ЃЉЃЌBЃЈ3ЃЌЉ1ЃЉДњШыЕУЃК ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК ![]() ЃЌЫљвджБЯпABЕФНтЮіЪНЮЊy=xЉ4ЃЛ
ЃЌЫљвджБЯпABЕФНтЮіЪНЮЊy=xЉ4ЃЛ
ЃЈ2ЃЉжБЯпABНЛxжсгкЕуQЃЌШчЭМЃЌЕБy=0ЪБЃЌxЉ4=0ЃЌНтЕУx=4ЃЌдђQЃЈ4ЃЌ0ЃЉЃЌвђЮЊPAЉPBЁмABЃЈЕБPЁЂAЁЂBЙВЯпЪБШЁЕШКХЃЉЃЌЫљвдЕБPЕудЫЖЏЕНQЕуЪБЃЌЯпЖЮPAгыЯпЖЮPBжЎВюДяЕНзюДѓЃЌДЫЪБPЕузјБъЮЊЃЈ4ЃЌ0ЃЉЃЎ
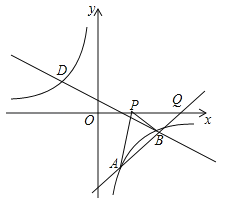
ПМЕуЃКЗДБШР§КЏЪ§гывЛДЮКЏЪ§ЕФНЛЕуЮЪЬтЃЎ
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
22
ЁОЬтФПЁПГЩЖМШ§ЪЅЯчЛЈЛмЛљЕиГіЪлСНжжХшддЛЈЛмЃКЬЋбєЛЈ6дЊ/ХшЃЌахЧђЛЈ10дЊ/ХшЃЎШєвЛДЮЙКТђЕФахЧђЛЈГЌЙ§20ХшЪБЃЌГЌЙ§20ХшВПЗжЕФахЧђЛЈМлИёДђ8елЃЎ
ЃЈ1ЃЉШєаЁеХМвЛЈЬЈТЬЛЏашгУ60ХшСНжжХшддЛЈЛмЃЌаЁеХАжАжИјЫћ460дЊЧЎШЅЙКТђЃЌЮЪСНжжЛЈЛмИїТђСЫЖрЩйХшЃП
ЃЈ2ЃЉЗжБ№аДГіСНжжЛЈЛмЕФИЖПюН№ЖюyЃЈдЊЃЉЙигкЙКТђСПxЃЈХшЃЉЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ3ЃЉЮЊСЫУРЛЏЛЗОГЃЌЛЈдАаЁЧјМЦЛЎЕНИУЛљЕиЙКТђетСНжжЛЈЛмЙВ90ХшЃЌЦфжаЬЋбєЛЈЪ§СПВЛГЌЙ§ахЧђЛЈЪ§СПЕФвЛАыЃЎСНжжЛЈЛмИїТђЖрЩйХшЪБЃЌзмЗбгУзюЩйЃЌзюЩйЗбгУЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
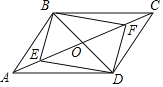
ЁОЬтФПЁПШчЭМЃЌ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() ЁЂ
ЁЂ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌХаЖЯЫФБпаЮ
ЃЌХаЖЯЫФБпаЮ![]() ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЕу![]() ЪЧвд
ЪЧвд![]() ЮЊжБОЖЕФАыдВ
ЮЊжБОЖЕФАыдВ![]() ЩЯШЮвтвЛЕу(ВЛгыЕу
ЩЯШЮвтвЛЕу(ВЛгыЕу![]() жиКЯ)ЃЌСЌНг
жиКЯ)ЃЌСЌНг![]() ВЂбгГЄжСЕу
ВЂбгГЄжСЕу![]() ЪЙ
ЪЙ![]() СЌНг
СЌНг![]() НЛАыдВ
НЛАыдВ![]() гкЕу
гкЕу![]() Й§Еу
Й§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ

![]() ЧѓжЄЃК
ЧѓжЄЃК![]() ЃЎ
ЃЎ
![]() ШчЭМ2ЃЌСЌНг
ШчЭМ2ЃЌСЌНг![]() ЃЎ
ЃЎ
ЂйЕБ![]()
![]() ЪБЃЌЫФБпаЮ
ЪБЃЌЫФБпаЮ![]() ЪЧСтаЮЃЛ
ЪЧСтаЮЃЛ
ЂкЕБ![]()
![]() ЪБЃЌЫФБпаЮ
ЪБЃЌЫФБпаЮ![]() ЪЧе§ЗНаЮЃЎ
ЪЧе§ЗНаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжгФЯЩНдКЪПЬИЕНЗРЛЄаТаЭЙкзДВЁЖОЗЮбзЪБЫЕЃКЁАЮвУЧашвЊжиЪгЗРЛЄЃЌЕЋвВВЛБиПжЛХЃЌОЁСПЩйШЅШЫдБУмМЏЕФГЁЫљЃЌГіУХДїПкежЃЌдкЪвФкзЂвтЭЈЗчЃЌЧкЯДЪжЃЌЖрдЫЖЏЃЌЩйАОвЙЃЎЁБФГЩчЧјЮЊСЫМгЧПЩчЧјОгУёЖдаТаЭЙкзДВЁЖОЗЮбзЗРЛЄжЊЪЖЕФСЫНтЃЌЭЈЙ§ЮЂаХШКаћДЋаТаЭЙкзДВЁЖОЗЮбзЕФЗРЛЄжЊЪЖЃЌВЂЙФРјЩчЧјОгУёдкЯпВЮгызїД№ЁЖ2020ФъаТаЭЙкзДВЁЖОЗРжЮШЋЙњЭГвЛПМЪдЃЈШЋЙњОэЃЉЁЗЪдОэЃЈТњЗж100ЗжЃЉЃЌЩчЧјЙмРэдБЫцЛњДгга400ШЫЕФФГаЁЧјГщШЁ40УћШЫдБЕФД№ОэГЩМЈЃЌВЂЖдЫћУЧЕФГЩМЈЃЈЕЅЮЛЃКЗжЃЉЭГМЦШчЯТЃК
85 | 80 | 95 | 100 | 90 | 95 | 85 | 65 | 75 | 85 |
90 | 90 | 70 | 90 | 100 | 80 | 80 | 90 | 95 | 75 |
80 | 60 | 80 | 95 | 85 | 100 | 90 | 85 | 85 | 80 |
95 | 75 | 80 | 90 | 70 | 80 | 95 | 75 | 100 | 90 |
ИљОнЪ§ОнЛцжЦСЫШчЯТЕФБэИёКЭЭГМЦЭМЃК
ЕШМЖ | ГЩМЈЃЈ | ЦЕТЪ | ЦЕТЪ |
|
| 10 | 0.25 |
|
|
| |
|
| 12 | 0.3 |
|
|
| |
КЯМЦ | 40 | 1 | |
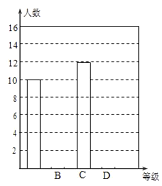
ИљОнЩЯУцЬсЙЉЕФаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЭГМЦБэжаЕФ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧыВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉИљОнГщбљЕїВщНсЙћЃЌЧыЙРМЦИУаЁЧјД№ЬтГЩМЈЮЊЁА![]() МЖЁБЕФгаЖрЩйШЫЃП
МЖЁБЕФгаЖрЩйШЫЃП
ЃЈ4ЃЉИУЩчЧјга2УћФаЙмРэдБКЭ2УћХЎЙмРэдБЃЌЯжДгжаЫцЛњЬєбЁ2УћЙмРэдБВЮМгЁАЩчЧјЗРПиЁБаћДЋЛюЖЏЃЌЧыгУЪїзДЭМЗЈЛђСаБэЗЈЧѓГіЧЁКУбЁжаЁА1Фа1ХЎЁБЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
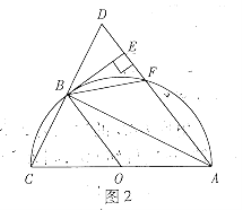
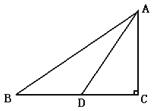
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯCЃН90ЁуЃЌADЪЧЁЯBACЕФЦНЗжЯпЃЌABЁУBDЃН![]() .
.
(1)ЧѓtanЁЯDACЕФжЕ.
(2)ШєBDЃН4ЃЌЧѓSЁїABC.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНШЫдквЛЬѕГЄЮЊ600mЕФБЪжБЕРТЗЩЯОљдШЕиХмВНЃЌЫйЖШЗжБ№ЮЊ![]() КЭ
КЭ![]() ЃЌЦ№ХмЧАввдкЦ№ЕуЃЌМздкввЧАУц50mДІЃЌШєСНШЫЭЌЪБЦ№ХмЃЌдђДгЦ№ХмГіЗЂЕНЦфжавЛШЫЯШЕНДяжеЕуЕФЙ§ГЬжаЃЌСНШЫжЎМфЕФОрРыy(m)гыЪБМфt(s)ЕФКЏЪ§ЭМЯѓЪЧЃЈ ЃЉ
ЃЌЦ№ХмЧАввдкЦ№ЕуЃЌМздкввЧАУц50mДІЃЌШєСНШЫЭЌЪБЦ№ХмЃЌдђДгЦ№ХмГіЗЂЕНЦфжавЛШЫЯШЕНДяжеЕуЕФЙ§ГЬжаЃЌСНШЫжЎМфЕФОрРыy(m)гыЪБМфt(s)ЕФКЏЪ§ЭМЯѓЪЧЃЈ ЃЉ
A.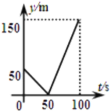 B.
B. C.
C.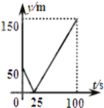 D.
D.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() жаЕуЃЌЕу
жаЕуЃЌЕу![]() дк
дк![]() бгГЄЯпЩЯЃЌ
бгГЄЯпЩЯЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЩш![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
ЂйШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЂкСЌНс![]() ЃЌЗжБ№МЧ
ЃЌЗжБ№МЧ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЎЃЈжБНгаДГіД№АИЃЉ
ЃЎЃЈжБНгаДГіД№АИЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com