
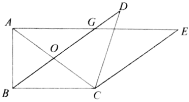
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 中点,点
中点,点![]() 在
在![]() 延长线上,
延长线上,![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)求证:![]() ;
;
(3)设![]() 交
交![]() 于点
于点![]() .
.
①若![]() ,
,![]() ,求
,求![]() 的值;
的值;
②连结![]() ,分别记
,分别记![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() ,
,![]() ,当
,当![]() 时,
时,![]() .(直接写出答案)
.(直接写出答案)
【答案】(1)详见解析;(2)详见解析;(3)①![]() ;②
;②![]() .
.
【解析】
(1)根据∠AOB=∠OBC+∠OCB,只要求出∠OBC,∠OCB即可.
(2)想办法证明CG⊥AE即可解决问题.
(3)①如图2中,作MH⊥CE于H,解直角三角形求出AG,GM,ME即可解决问题.
②如图3所示:连接DE.首先证明四边形OCED是平行四边形,再证明EC=2DG,利用平行线分线段成比例定理即可解决问题.
解:(1)∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,![]() 为
为![]() 中点,
中点,
∴![]() .
.
∴![]() .
.
∴![]() .即
.即![]() .
.
∴![]() .
.
(2)连结![]() (如图1).
(如图1).

∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴四边形![]() 为矩形.
为矩形.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
(3)①作![]() 于
于![]() (如图2).
(如图2).

由![]() ,
,![]() ,
,
则四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
②如图3所示:连接DE.

∵OA=OC,∠ABC=90°,
∴BO=OA=OC,
∴∠OBC=∠OCB,
∵AE∥BC,
∴∠CAE=∠ACB,∠AGO=∠OBC,
∵CA=CE,
∴∠CAE=∠CAE,
∴∠AGB=∠AEC,
∴AD∥CE,
∵DE∥AC,
∴四边形OCED是平行四边形,
∴OD=CE=CA,
∵∠OAG=∠OGA,
∴OA=OG,
∴OA=OC=OG=DG,
∵DG∥EC,
∴![]() ,
,
∴![]() ,
,
设S2=m,则S3=2m,
∴S△DGE=3m,
∵OG=GD,∠AGO=∠DGE,∠OAG=∠DEG,
∴△AGO≌△EGD(AAS),
∴S△AOG=S△DEG=3m,
∵OB=OG,
∴S△ABG=2S△AOG=6m,
∴S1:S2:S3=6m:m:2m=6:1:2.
故答案为:6:1:2.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】当图形具有邻边相等的特征时,我们可以把图形的一部分绕着公共端点旋转,这样将分散的条件集中起来,从而达到解决问题的目的
![]() 如图1,等腰直角三角形
如图1,等腰直角三角形![]() 内有一点
内有一点![]() 连接
连接![]() 为探究
为探究![]() 三条线段间的数量关系,我们可以将
三条线段间的数量关系,我们可以将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() 连接
连接![]() 则
则![]() ___ ____
___ ____![]() 是_ 三角形,
是_ 三角形,![]() 三条线段的数量关系是_ ;
三条线段的数量关系是_ ;
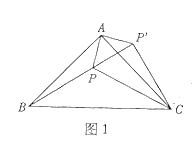
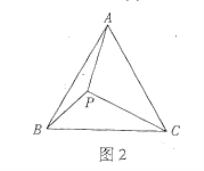
![]() 如图2,等边三角形
如图2,等边三角形![]() 内一点P,连接
内一点P,连接![]() 请借助第一问的方法探究
请借助第一问的方法探究![]() 三条线段间的数量关系.
三条线段间的数量关系.
![]() 如图3 ,在四边形
如图3 ,在四边形![]() 中,
中,![]() 点
点![]() 在四边形内部,且
在四边形内部,且![]()
![]() 请直接写出
请直接写出![]() 的长.
的长.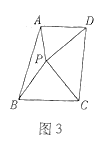
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高淳固城湖大桥采用H型塔型斜拉桥结构(如甲图),图乙是从图甲抽象出的平面图.测得拉索AB与水平桥面的夹角是45°,拉索CD与水平桥面的夹角是65°,两拉索顶端的距离AC为2米,两拉索底端距离BD为10米,请求出立柱AH的长(结果精确到0.1米).

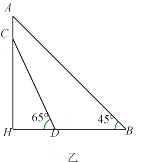
(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学共有3个一样规模的大餐厅和2个一样规模的小餐厅,经过测试同时开放2个大餐厅和1个小餐厅,可供3000名学生就餐;同时开放1个大餐厅,1个小餐厅,可供1700名学生就餐.
(1)请问1个大餐厅、1个小餐厅分别可供多少名学生就餐.
(2)如果3个大餐厅和2个小餐厅全部开放,那么能否供全校4500名学生就餐?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.

(1)求证:△AEC≌△ADB;(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在艺术节宣传活动中,采用了四种宣传形式:A唱歌、B舞蹈、C朗诵、D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:

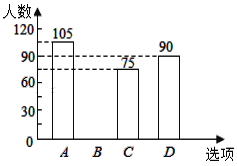
请结合统计图表,回答下列问题:
(1)本次调查的学生共____人,a=______, 并将条形统计图补充完整;
(2)如果该校学生有2000人,请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人?
(3)学校采用调查方式让每班在A、B、C、D四种宣传形式中,随机抽取两种进行展示,请用树状图或列表法,求某班抽到的两种形式有一种是“唱歌”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列对于随机事件的概率的描述:
①抛掷一枚均匀的硬币,因为“正面朝上”的概率是0.5,所以抛掷该硬币100次时,就会有50次“正面朝上”;
②一个不透明的袋子里装有4个黑球,1个白球,这些球除了颜色外无其他差别.从中随机摸出一个球,恰好是白球的概率是0.2;
③测试某射击运动员在同一条件下的成绩,随着射击次数的增加,“射中9环以上”的频率总是在0.85附近摆动,显示出一定的稳定性,可以估计该运动员“射中9环以上”的概率是0.85
其中合理的有______(只填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料一:一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数,否则称为合数.
其中,1和0既不是质数也不是合数.
材料二:一个较大自然数是质数还是合数通常用“![]() 法”来判断,主要分为三个步骤:
法”来判断,主要分为三个步骤:
第一步,找出大于![]() 且最接近
且最接近![]() 的平方数
的平方数![]() ;
;
第二步,用小于![]() 的所有质数去除
的所有质数去除![]() ;
;
第三步,如果这些质数都不能整除![]() ,那么
,那么![]() 是质数;如果这些质数中至少有一个能整除
是质数;如果这些质数中至少有一个能整除![]() ,那么
,那么![]() 就是合数.
就是合数.
如何判断239是质数还是合数?
第一步,![]() ;
;
第二步,小于16的质数有:2、3、5、7、11、13,用2、3、5、7、11、13依次去除239;
第三步,发现没有质数能整除239,所以239是质数.
材料三:分解质因数就是把一个合数分解成若干个质数的乘积的形式,通过分解质因数可以确定该合数的约数的个数.若![]() …(
…(![]() ,
,![]() ,
,![]() …是不相等的质数,
…是不相等的质数,![]() ,
,![]() ,
,![]() …是正整数),则合数
…是正整数),则合数![]() 共有
共有![]() …个约数.如
…个约数.如![]() ,
,![]() ,则8共有4个约数;又如
,则8共有4个约数;又如![]() ,
,![]() ,则12共有6个约数.请用以上方法解决下列问题:
,则12共有6个约数.请用以上方法解决下列问题:
(1)请用“![]() 法”判断163是质数还是合数;
法”判断163是质数还是合数;
(2)求有12个约数的最小自然数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com