
如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1。
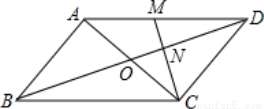
(1)求BD的长
(2)若△DCN的面积为2,求四边形ABNM的面积。
(1)6;(2)5.
【解析】
试题分析:(1)根据平行四边形的性质得AD∥BC,从而△MND∽△CNB,结合M为AD中点,可得BN=2DN,又OB=OD,ON=1,所以可求出BD=6;(2)利用△MND∽△CNB,得MN:CN=DN:BN=1:2,从而可得S△BNC=2S△CND=4,S△MND=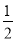 S△CND=1,所以S△ABD=S△BCD=6,然后根据S四边形ABNM=S△ABD- S△MND
S△CND=1,所以S△ABD=S△BCD=6,然后根据S四边形ABNM=S△ABD- S△MND
可解.
试题解析:解(1)∵平行四边形ABCD,∴AD∥BC,AD=BC,OB=OD,
∴∠DMN=∠BCN,∠MDN=∠NBC;∴△MND∽△CNB, 2分
∴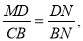 ∵M为AD中点,∴MD=
∵M为AD中点,∴MD=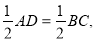
即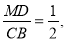 ∴
∴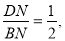 即BN=2DN, 4分
即BN=2DN, 4分
设OB=OD=x,则有BD=2x,BN=OB+ON=x+1,DN=x-1, 6分
∴x+1=2(x-1),解得:x=3 ∴BD=2x=6 8分
(2) ∵△MND∽△CNB,且相似比为1:2,∴MN:CN=DN:BN=1:2
∴S△MND=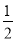 S△CND=1,S△BNC=2S△CND=4。 10分
S△CND=1,S△BNC=2S△CND=4。 10分
∴S△ABD=S△BCD= S△BCN+S△CND=4+2=6
∴S四边形ABNM=S△ABD- S△MND =6-1=5 12分
考点:1.平行四边形的性质;2.相似三角形的判定与性质.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源:2014-2015学年山东省诸城市九年级下学期开学检测数学试卷(解析版) 题型:解答题
(本题满分10分)如图所示的粮仓可以看成圆柱体与圆锥体的组合体,已知其底面半径为6米,高为4米,下方圆柱高为3米.
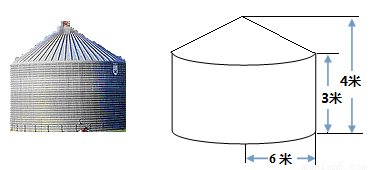
(1)求该粮仓的容积;
(2)求上方圆锥的侧面积.(计算结果保留根号)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期期末考试数学试卷(解析版) 题型:选择题
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( )
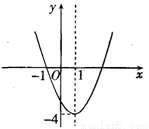
A.函数y=ax2+bx+c(a≠0)的最小值是-4;
B.-1和3是方程ax2+bx+c=0(a≠0)的两个实数根;
C.当x<1时,y随x的增大而增大;
D.当x≤-1或x≥3时,不等式ax2+bx+c≥0成立.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省铜陵市四校九年级2月开学联考数学试卷(解析版) 题型:填空题
如果圆锥的底面周长是20π,侧面展开后所得的扇形的圆心角为120°,那么圆锥的侧面积是__________.(结果保留π)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省铜陵市四校九年级2月开学联考数学试卷(解析版) 题型:选择题
把函数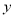 =f(x)=
=f(x)=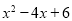 的图象向左平移1个单位,再向上平移1个单位,所得图象对
的图象向左平移1个单位,再向上平移1个单位,所得图象对
应的函数的解析式是( )
A.y=(x-3)2+3 B.y=(x-3)2+1
C.y=(x-1)2+3 D.y=(x-1)2+1
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省安庆市毕业班正月联考数学试卷(解析版) 题型:解答题
如图,用一根6米长的笔直钢管弯折成如图所示的路灯杆ABC,AB垂直于地面,线段AB与线段BC所成的角∠ABC=120°,若路灯杆顶端C到地面的距离CD=5.5米,求AB长.
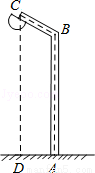
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省安庆市毕业班正月联考数学试卷(解析版) 题型:选择题
二次函数y=ax2+bx+c(a≠0)的图象如图,关于该二次函数,下列说法错误的是( )
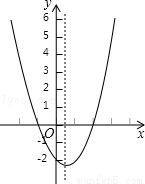
A.函数有最小值
B.对称轴是直线
C.当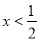 时,y随x的增大而减小
时,y随x的增大而减小
D.当﹣1<x<2时,y>0
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省牡丹江管理局北斗星协会九年级中考二模数学试卷(解析版) 题型:解答题
(本题满分5分)先化简(1+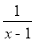 )÷
)÷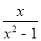 ,再选择一个恰当的x值代人并求值.
,再选择一个恰当的x值代人并求值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市七年级上学期期中考试数学试卷(解析版) 题型:选择题
将正整数1,2,3,4……按以下方式排列
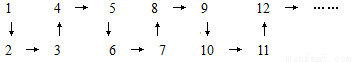
根据排列规律,从2010到2012的箭头依次为
A.↓ → B.→ ↓ C.↑ → D. → ↑
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com