
分析 ①根据负整数指数幂的意义进行计算即可;
②化成积的乘方的形式进行二次根式的运算;
③根据负整数指数幂的意义进行计算,然后进行化简即可.
解答 解:①${({-\sqrt{15}})^{-2}}$=$\frac{1}{(-{\sqrt{15})}^{2}}$=$\frac{1}{15}$;
②${({\sqrt{15}+4})^{2015}}{({\sqrt{15}-4})^{2016}}$
=($\sqrt{15}$+4)2015($\sqrt{15}$-4)2015($\sqrt{15}$-4)
=[($\sqrt{15}$+4)($\sqrt{15}$-4)]2015($\sqrt{15}$-4)
=-($\sqrt{15}$-4)
=4-$\sqrt{15}$;
③${({\sqrt{2}-1})^{-1}}$=$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}$+1.
故答案为$\frac{1}{15}$;4-$\sqrt{15}$;$\sqrt{2}$+1.
点评 此题考查了负整数指数幂的运算和二次根式的混合运算,注意在计算负整数指数幂时,一定要根据负整数指数幂的意义计算.


科目:初中数学 来源: 题型:解答题
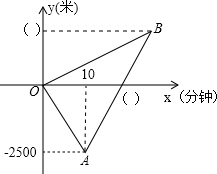 早上小芳和妈妈同时从家里出发,小芳步行上学、妈妈骑自行车上班,两人的行进方向正好相反,规定从家往学校的方向为正,如图是她们离家的距离y(米)与时间x(分钟)之间的函数图象,妈妈骑车走了10分钟时接到小芳的电话,立即以原速度前往学校,若已知小芳步行的速度为50米/分钟,并且妈妈与小芳同时到达学校.
早上小芳和妈妈同时从家里出发,小芳步行上学、妈妈骑自行车上班,两人的行进方向正好相反,规定从家往学校的方向为正,如图是她们离家的距离y(米)与时间x(分钟)之间的函数图象,妈妈骑车走了10分钟时接到小芳的电话,立即以原速度前往学校,若已知小芳步行的速度为50米/分钟,并且妈妈与小芳同时到达学校.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
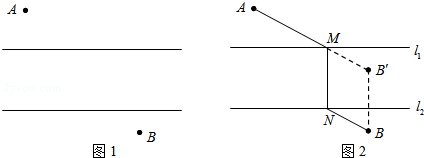
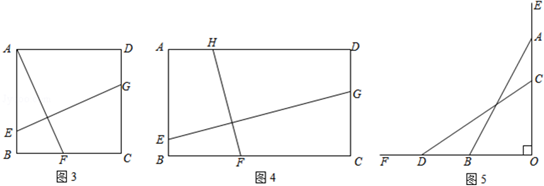
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
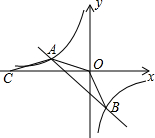 如图,直线AB与反比例函数的图象交于A(-4,m)、B(2,n)两点,点C在x轴上,AO=AC,△OAC的面积为8.
如图,直线AB与反比例函数的图象交于A(-4,m)、B(2,n)两点,点C在x轴上,AO=AC,△OAC的面积为8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com