
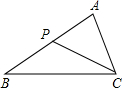
 如图,点P是△ABC的边AB上的一点,下列条件中不能得到△ACP∽△ABC的是( )
如图,点P是△ABC的边AB上的一点,下列条件中不能得到△ACP∽△ABC的是( )| A. | ∠ACP=∠B | B. | ∠APC=∠ACB | C. | $\frac{AP}{AC}=\frac{AC}{AB}$ | D. | $\frac{AP}{AC}=\frac{PC}{CB}$ |
分析 根据相似三角形的性质即可进行解答.
解答 解:A、∵∠ACP=∠B,两角为对应角,∴可判定△ACP∽△ABC,故本选项错误;
B、∵∠APC=∠ACB,两角为对应角,∴可判定△ACP∽△ABC,故本选项错误;
C、∵$\frac{AP}{AC}$=$\frac{AC}{AB}$,两边为对应边且∠A为对应角,∴可判定△ACP∽△ABC,故本选项错误;
D、∵$\frac{AP}{AC}$=$\frac{PC}{AB}$,缺少一个对应角,∴不可判定△ACP∽△ABC,故本选项正确;
故选D.
点评 本题考查相似三角形的判定.要找的对应边与对应角,公共角是很重要的一个量,要灵活加以利用.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | b是a、c的比例中项,且a:b=7:3,则b:c=7:3 | |
| B. | 正三角形、菱形、矩形中,对称轴最多的是菱形 | |
| C. | 如果点C是线段的黄金分割点,那么AC=0.618AB | |
| D. | 相似图形一定是位似图形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 每周做家务的时间(小时) | 0 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 合计 |
| 人数 | 2 | 2 | 6 | 12 | 13 | 4 | 3 | 50 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com