
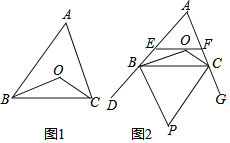
【题目】已知:△ABC中,BO平分∠ABC,CO平分∠ACB
(1)如图1,∠BOC和∠A有怎样的数量关系?请说明理由
(2)如图2,过O点的直线分别交△ABC的边AB、AC于E、F(点E不与A,B重合,点F不与A、C重合),BP平分外角∠DBC,CP平分外角∠GCB,BP,CP相交于P.求证:∠P=∠BOE+∠COF;
(3)如果(2)中过O点的直线与AB交于E(点E不与A、B重合),与CA的延长线交于F在其它条件不变的情况下,请直接写出∠P、∠BOE、∠COF三个角之间的数量关系.
【答案】(1)∠BOC=90°+![]() ∠A,理由详见解析;(2)详见解析;(3)∠BOE+∠COF﹣∠P=180°.
∠A,理由详见解析;(2)详见解析;(3)∠BOE+∠COF﹣∠P=180°.
【解析】
(1)根据三角形的内角和等于180°求出∠ABC+∠ACB的度数,再根据角平分线的定义求出∠OBC+∠OCB的度数,然后利用三角形的内角和等于180°列式计算即可得解;
(2)证明∠P=90°﹣![]() ∠A,得到∠P+∠BOC=180°即可解决问题;
∠A,得到∠P+∠BOC=180°即可解决问题;
(3)画出图形由∠P+∠BOC=180°,∠BOC+∠BOE+∠COF=360°,可得∠BOE+∠COF﹣∠P=180°.
解:(1)∵∠ABC+∠ACB=180°﹣∠A,BO平分∠ABC,CO平分∠ACB,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠OBC+∠OCB
=![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
=![]() (180°﹣∠A)
(180°﹣∠A)
=90°﹣![]() ∠A,
∠A,
在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)=90°+![]() ∠A;
∠A;
(2)∵BP、CP分别平分外角∠DBC、∠GCB,
∴∠PBC=![]() ∠CBD,∠PCB=
∠CBD,∠PCB=![]() ∠BCG,
∠BCG,
∴∠P=180°﹣∠CBP﹣∠BCP)
=180°﹣![]() (∠CBD+∠BCG)
(∠CBD+∠BCG)
=180°﹣![]() (∠A+∠ACB+∠A+∠ABC)
(∠A+∠ACB+∠A+∠ABC)
=180°﹣![]() (180°+∠A)
(180°+∠A)
=90°﹣![]() ∠A,
∠A,
∴∠P+∠BOC=180°,
∵∠BOC+∠BOE+∠COF=180°,
∴∠P=∠BOE+∠COF;
(3)如图3中,
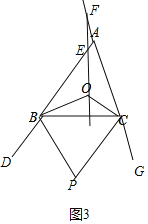
∵∠P+∠BOC=180°,∠BOC+∠BOE+∠COF=360°,
∴∠BOE+∠COF﹣∠P=180°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
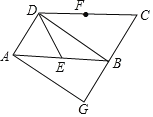
【题目】如图,ABCD中,∠ADC=120°,AD![]() AB,E、F分别是AB、CD的中点,过点A作AG∥BD,交CB的延长线于点G.
AB,E、F分别是AB、CD的中点,过点A作AG∥BD,交CB的延长线于点G.
(1)求证:DE=BE;
(2)请判断四边形AGBD是什么特殊的四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() (0,
(0,![]() ),
),![]() (3,4).
(3,4).
(1)求抛物线的表达式及对称轴;
(2)设点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() 是抛物线对称轴上一动点,记抛物线在
是抛物线对称轴上一动点,记抛物线在![]() ,
,![]() 之间的部分为图象
之间的部分为图象![]() (包含
(包含![]() ,
,![]() 两点).若直线
两点).若直线![]() 与图象
与图象![]() 有公共点,结合函数图像,求点
有公共点,结合函数图像,求点![]() 纵坐标
纵坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)如图所示,下列结论中:
①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1).
其中正确的结论有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,菱形OABC的边长为2,点A在第一象限,点C在x轴正半轴上,∠AOC=60°,若将菱形OABC绕点O顺时针旋转75°,得到四边形OA′B′C′,则点B的对应点B′的坐标为_____.
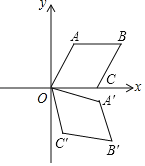
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b的图像与x轴和y轴的正半轴分别交于A,B两点.已知OA+OB=6(O为坐标原点),且![]() =4,则这个一次函数的解析式为 ( )
=4,则这个一次函数的解析式为 ( )
A.y=-![]() x+2B.y=-2x+4
x+2B.y=-2x+4
C.y=![]() x+2D.y=-
x+2D.y=-![]() x+2或y=-2x+4
x+2或y=-2x+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象对称轴为
的图象对称轴为![]() ,图象交x轴于A,B,交y轴于
,图象交x轴于A,B,交y轴于![]() ,且
,且![]() ,直线
,直线![]() 与二次函数图象交于M,
与二次函数图象交于M,![]() 在N的右边
在N的右边![]() ,交y轴于P.
,交y轴于P.
![]() 求二次函数图象的解析式;
求二次函数图象的解析式;
![]() 若
若![]() ,且
,且![]() 的面积为3,求k的值;
的面积为3,求k的值;
![]() 若
若![]() ,直线AN交y轴于Q,求
,直线AN交y轴于Q,求![]() 的值或取值范围.
的值或取值范围.
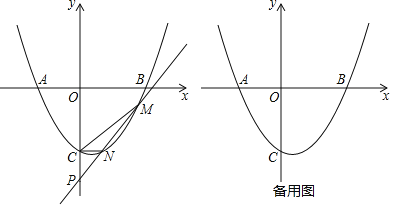
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com