
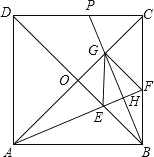
【题目】如图,正方形ABCD中,对角线AC、BD交于点O,∠BAC的平分线交BD于E,交BC于F,BH⊥AF于H,交AC于G,交CD于P,连接GE、GF,以下结论:①△OAE≌△OBG;②四边形BEGF是菱形;③BE=CG;④![]() ﹣1;⑤S△PBC:S△AFC=1:2,其中正确的有( )个.
﹣1;⑤S△PBC:S△AFC=1:2,其中正确的有( )个.
A.2B.3C.4D.5
【答案】C
【解析】
根据AF是∠BAC的平分线,BH⊥AF,可证AF为BG的垂直平分线,然后再根据正方形内角及角平分线进行角度转换证明EG=EB,FG=FB,即可判定②选项;设OA=OB=OC=a,菱形BEGF的边长为b,由四边形BEGF是菱形转换得到CF=![]() GF=
GF=![]() BF,由四边形ABCD是正方形和角度转换证明△OAE≌△OBG,即可判定①;则△GOE是等腰直角三角形,得到GE=
BF,由四边形ABCD是正方形和角度转换证明△OAE≌△OBG,即可判定①;则△GOE是等腰直角三角形,得到GE=![]() OG,整理得出a,b的关系式,再由△PGC∽△BGA,得到
OG,整理得出a,b的关系式,再由△PGC∽△BGA,得到![]() =1+
=1+![]() ,从而判断得出④;得出∠EAB=∠GBC从而证明△EAB≌△GBC,即可判定③;证明△FAB≌△PBC得到BF=CP,即可求出
,从而判断得出④;得出∠EAB=∠GBC从而证明△EAB≌△GBC,即可判定③;证明△FAB≌△PBC得到BF=CP,即可求出![]() ,从而判断⑤.
,从而判断⑤.
解:∵AF是∠BAC的平分线,
∴∠GAH=∠BAH,
∵BH⊥AF,
∴∠AHG=∠AHB=90°,
在△AHG和△AHB中
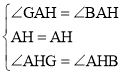 ,
,
∴△AHG≌△AHB(ASA),
∴GH=BH,
∴AF是线段BG的垂直平分线,
∴EG=EB,FG=FB,
∵四边形ABCD是正方形,
∴∠BAF=∠CAF=![]() ×45°=22.5°,∠ABE=45°,∠ABF=90°,
×45°=22.5°,∠ABE=45°,∠ABF=90°,
∴∠BEF=∠BAF+∠ABE=67.5°,∠BFE=90°﹣∠BAF=67.5°,
∴∠BEF=∠BFE,
∴EB=FB,
∴EG=EB=FB=FG,
∴四边形BEGF是菱形;②正确;
设OA=OB=OC=a,菱形BEGF的边长为b,
∵四边形BEGF是菱形,
∴GF∥OB,
∴∠CGF=∠COB=90°,
∴∠GFC=∠GCF=45°,
∴CG=GF=b,∠CGF=90°,
∴CF=![]() GF=
GF=![]() BF,
BF,
∵四边形ABCD是正方形,
∴OA=OB,∠AOE=∠BOG=90°,
∵BH⊥AF,
∴∠GAH+∠AGH=90°=∠OBG+∠AGH,
∴∠OAE=∠OBG,
在△OAE和△OBG中
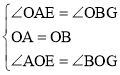 ,
,
∴△OAE≌△OBG(ASA),①正确;
∴OG=OE=a﹣b,
∴△GOE是等腰直角三角形,
∴GE=![]() OG,
OG,
∴b=![]() (a﹣b),
(a﹣b),
整理得a=![]() b,
b,
∴AC=2a=(2+![]() )b,AG=AC﹣CG=(1+
)b,AG=AC﹣CG=(1+![]() )b,
)b,
∵四边形ABCD是正方形,
∴PC∥AB,
∴![]() =
=![]() =
=![]() =1+
=1+![]() ,
,
∵△OAE≌△OBG,
∴AE=BG,
∴![]() =1+
=1+![]() ,
,
∴![]() =
=![]() =1﹣
=1﹣![]() ,④正确;
,④正确;
∵∠OAE=∠OBG,∠CAB=∠DBC=45°,
∴∠EAB=∠GBC,
在△EAB和△GBC中
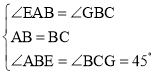 ,
,
∴△EAB≌△GBC(ASA),
∴BE=CG,③正确;
在△FAB和△PBC中
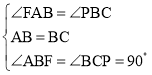 ,
,
∴△FAB≌△PBC(ASA),
∴BF=CP,
∴![]() =
=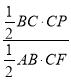 =
=![]() =
=![]() =
=![]() ,⑤错误;
,⑤错误;
综上所述,正确的有4个,
故选:C.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2﹣x+c的对称轴为直线x=1,与x轴的一个交点为A(﹣1,0),顶点为B.点C(5,m)在抛物线上,直线BC交x轴于点E.
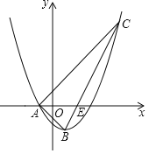
(1)求抛物线的表达式及点E的坐标;
(2)联结AB,求∠B的正切值;
(3)点G为线段AC上一点,过点G作CB的垂线交x轴于点M(位于点E右侧),当△CGM与△ABE相似时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绿色出行是对环境影响最小的出行方式,“共享单车”已成为北京的一道靓丽的风景线.某社会实践活动小
组为了了解“共享单车”的使用情况,对本校教师在3月6日至3月10日使用单车的情况进行了问卷调查,
以下是根据调查结果绘制的统计图的一部分:
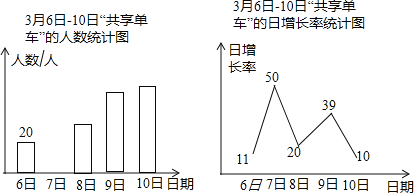
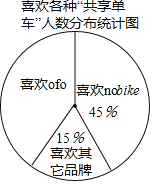
请根据以上信息解答下列问题:
(1)3月7日使用“共享单车”的教师人数为人,并请补全条形统计图;
(2)不同品牌的“共享单车”各具特色,社会实践活动小组针对有过使用“共享单车”经历的教师做了进一步调查,每位教师都按要求选择了一种自己喜欢的“共享单车”,统计结果如图,其中喜欢![]() 的教师有36人,求喜欢
的教师有36人,求喜欢![]() 的教师的人数.
的教师的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A = 30°,AB = m,CD是边AB上的中线,将△ACD沿CD所在直线翻折,得到△ECD,若△ECD与△ABC重合部分的面积等于△ABC面积的![]() ,则△ABC的面积为___________(用m的代数式表示).
,则△ABC的面积为___________(用m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
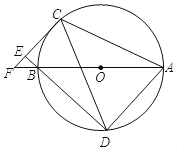
【题目】如图,AB为⊙O的直径,C、D为⊙O上异于A、B的两点,连接CD,过点C作CE⊥DB,交CD的延长线于点E,垂足为点E,直径AB与CE的延长线相交于点F.
(1)连接AC,AD,求证:∠DAC+∠ACF=180°;
(2)若∠ABD=2∠BDC,
①求证:CF是⊙O的切线;
②当BD=6,tanF=![]() 时,求CF的长.
时,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
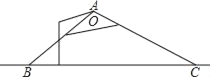
【题目】如图,一盏路灯沿灯罩边缘射出的光线与地面BC交于点B、C,测得∠ABC=45°,∠ACB=30°,且BC=20米.
(1)请用圆规和直尺画出路灯A到地面BC的距离AD;(不要求写出画法,但要保留作图痕迹)
(2)求出路灯A离地面的高度AD.(精确到0.1米)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,将
的中点,将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() .
.
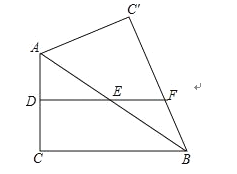
(1)判断![]() 的形状为 ;
的形状为 ;
(2)当![]() 时,求证四边形
时,求证四边形![]() 为正方形;
为正方形;
(3)若![]() ,连接
,连接![]() ,当
,当![]() 时,直接写出
时,直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某区域部分交通线路图,其中直线![]() ,直线
,直线![]() 与直线
与直线![]() 、
、![]() 、
、![]() 都垂直,垂足分别点
都垂直,垂足分别点![]() 、点
、点![]() 和点
和点![]() ,(高速路右侧边缘),
,(高速路右侧边缘),![]() 上的点
上的点![]() 位于点
位于点![]() 的北偏东
的北偏东![]() 方向上,且
方向上,且![]() 千米,
千米,![]() 上的点
上的点![]() 位于点
位于点![]() 的北偏东
的北偏东![]() 方向上,且
方向上,且![]() ,
,![]() 千米.点
千米.点![]() 和点
和点![]() 是城际线
是城际线![]() 上的两个相邻的站点.
上的两个相邻的站点.
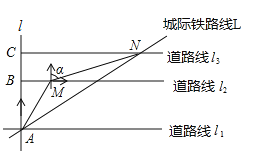
(1)求![]() 和
和![]() 之间的距离;
之间的距离;
(2)若城际火车平均时速为![]() 千米/小吋,求市民小强乘坐城际火车从站点
千米/小吋,求市民小强乘坐城际火车从站点![]() 到站点
到站点![]() 需要多少小时?(结果用分数表示)
需要多少小时?(结果用分数表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线l1:y=mx(m≠0) 与直线l2:y=ax+b(a≠0) 相交于点 A(1,2),直线l2与 x轴交于点B(3,0).
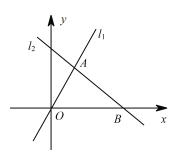
(1)分别求直线l1 和l2的表达式;
(2)过动点P(0,n)且平行于x轴的直线与l1 ,l2的交点分别为C ,D,当点 C 位于点 D 左方时,写出 n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com