
【题目】如图,已知抛物线y=ax2﹣x+c的对称轴为直线x=1,与x轴的一个交点为A(﹣1,0),顶点为B.点C(5,m)在抛物线上,直线BC交x轴于点E.
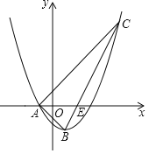
(1)求抛物线的表达式及点E的坐标;
(2)联结AB,求∠B的正切值;
(3)点G为线段AC上一点,过点G作CB的垂线交x轴于点M(位于点E右侧),当△CGM与△ABE相似时,求点M的坐标.
【答案】(1)![]() ,E(2,0);(2)3;(3) M点的坐标为(5,0)或(7,0)
,E(2,0);(2)3;(3) M点的坐标为(5,0)或(7,0)
【解析】
(1)由对称轴可求得a的值,再把A点坐标代入可求得c的值,则可求得抛物线表达式,则可求出B、C的坐标,由待定系数法可求得直线BC的解析式,可求出E的坐标
(2)由A、B、C三点的坐标可求得AB、AC和BC的长,可判定△ABC是以BC为斜边的直角三角形,利用三角形的定义可求出答案
(3)设M(x,0),当∠GCM=∠BAE时,可知△AMC为等腰直角三角形,可求的M点的坐标;当∠CMG=∠BAE时,可证得△MEC∽△MCA,利用相似三角形的性质可求得x的值,可求得M点的坐标
(1)∵抛物线对称轴为x=1,
∴![]() ,解得
,解得![]() ,
,
把A点坐标代入可得![]() ,解得
,解得![]() ,
,
∴抛物线表达式为![]() ,
,
∵![]() ,
,
∴B(1,﹣2),
把C(5,m)代入抛物线解析式可得![]() ,
,
∴C(5,6),
设直线BC解析式为y=kx+b,
把B、C坐标代入可得![]() ,解得
,解得![]() ,
,
∴直线BC解析式为y=2x﹣4,
令y=2可得2x﹣4=0,解得x=2,
∴E(2,0);
(2)∵A(﹣1,0),B(1,﹣2),C(5,6),
∴![]() ,
,
∴AB2+AC2=8+72=80=BC2,
∴△ABC是以BC为斜边的直角三角形,
∴![]() ;
;
(3)∵A(﹣1,0),B(1,﹣2),
∴∠CAE=∠BAE=45°,
∵GM⊥BC,
∴∠CGM+∠GCB=∠GCB+∠ABC=90°,
∴∠CGM=∠ABC,
∴当△CGM与△ABE相似时有两种情况,
设M(x,0),则C(x,2x﹣4),
①当∠GCM=∠BAE=45°时,则∠AMC=90°,
∴MC=AM,即2x﹣4=x+1,解得x=5,
∴M(5,0);
②当∠GMC=∠BAE=∠MAC=45°时,
∵∠MEC=∠AEB=∠MCG,
∴△MEC∽△MCA,
∴![]() ,即
,即![]() ,
,
∴MC2=(x﹣2)(x+1),
∵C(5,6),
∴MC2=(x﹣5)2+62=x2﹣10x+61,
∴(x﹣2)(x+1)=x2﹣10x+61,解得x=7,
∴M(7,0);
综上可知M点的坐标为(5,0)或(7,0).


科目:初中数学 来源: 题型:
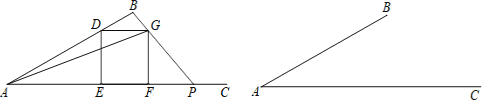
【题目】如图1,![]() 的余切值为2,
的余切值为2,![]() ,点D是线段
,点D是线段![]() 上的一动点(点D不与点A、B重合),以点D为顶点的正方形
上的一动点(点D不与点A、B重合),以点D为顶点的正方形![]() 的另两个顶点E、F都在射线
的另两个顶点E、F都在射线![]() 上,且点F在点E的右侧,联结
上,且点F在点E的右侧,联结![]() ,并延长
,并延长![]() ,交射线
,交射线![]() 于点P.
于点P.
(1)点D在运动时,下列的线段和角中,________是始终保持不变的量(填序号);
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;⑥
;⑥![]() ;
;
(2)设正方形的边长为x,线段![]() 的长为y,求y与x之间的函数关系式,并写出定义域;
的长为y,求y与x之间的函数关系式,并写出定义域;
(3)如果![]() 与
与![]() 相似,但面积不相等,求此时正方形的边长.
相似,但面积不相等,求此时正方形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
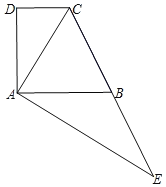
【题目】已知:如图,梯形ABCD,DC∥AB,对角线AC平分∠BCD,点E在边CB的延长线上,EA⊥AC,垂足为点A.
(1)求证:B是EC的中点;
(2)分别延长CD、EA相交于点F,若AC2=DCEC,求证:AD:AF=AC:FC.
查看答案和解析>>
科目:初中数学 来源: 题型:
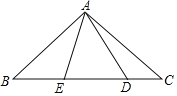
【题目】如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB.设BE=a,DC=b,那么AB=_____.(用含a、b的式子表示AB)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() 与x轴、y轴分别交于A、B两点,设O为坐标原点.
与x轴、y轴分别交于A、B两点,设O为坐标原点.
(1)求∠ABO的正切值;
(2)如果点A向左平移12个单位到点C,直线l过点C且与直线![]() 平行,求直线l的解析式.
平行,求直线l的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某足球特色学校在商场购买甲、乙两种品牌的足球.已知乙种足球比甲种足球每只贵20元,该校分别花费2000元、1400元购买甲、乙两种足球,这样购得甲种足球的数量是购得乙种足球数量的2倍,求甲、乙两种足球的单价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,联结DE并延长至点F,使EF=AE,联结AF,CF,联结BE并延长交CF于点G.
(1)求证:BC=DF;
(2)若BD=2DC,求证:GF=2EG;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学完二元一次方程组的应用之后,老师写出了一个方程组如下:![]() ,要求把这个方程组赋予实际情境.
,要求把这个方程组赋予实际情境.
小军说出了一个情境:学校有两个课外小组,书法组和美术组,其中书法组的人数的二倍比美术组多5人,书法组平均每人完成了4幅书法作品,美术组平均每人完成了3幅美术作品,两个小组共完成了40幅作品,问书法组和美术组各有多少人?
小明通过验证后发现小军赋予的情境有问题,请找出问题在哪?
查看答案和解析>>
科目:初中数学 来源: 题型:
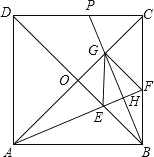
【题目】如图,正方形ABCD中,对角线AC、BD交于点O,∠BAC的平分线交BD于E,交BC于F,BH⊥AF于H,交AC于G,交CD于P,连接GE、GF,以下结论:①△OAE≌△OBG;②四边形BEGF是菱形;③BE=CG;④![]() ﹣1;⑤S△PBC:S△AFC=1:2,其中正确的有( )个.
﹣1;⑤S△PBC:S△AFC=1:2,其中正确的有( )个.
A.2B.3C.4D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com