
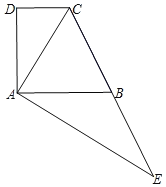
【题目】已知:如图,梯形ABCD,DC∥AB,对角线AC平分∠BCD,点E在边CB的延长线上,EA⊥AC,垂足为点A.
(1)求证:B是EC的中点;
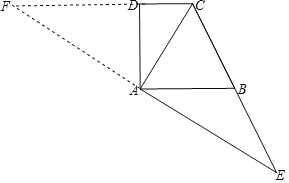
(2)分别延长CD、EA相交于点F,若AC2=DCEC,求证:AD:AF=AC:FC.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据平行线的性质结合角平分线的性质可得出∠BCA=∠BAC,进而可得出BA=BC,根据等角的余角相等结合等角对等边,即可得出AB=BE,进而可得出BE=BA=BC,此题得证;
(2)根据AC2=DCEC结合∠ACD=∠ECA可得出△ACD∽△ECA,根据相似三角形的性质可得出∠ADC=∠EAC=90°,进而可得出∠FDA=∠FAC=90°,结合∠AFD=∠CFA可得出△AFD∽△CFA,再利用相似三角形的性质可证出AD:AF=AC:FC.
(1)∵DC∥AB,∴∠DCA=∠BAC.
∵AC平分∠BCD,∴∠BCA=∠BAC=∠DCA,∴BA=BC.
∵∠BAC+∠BAE=90°,∠ACB+∠E =90°,∴∠BAE=∠E,∴AB=BE,∴BE=BA=BC,∴B是EC的中点;
(2)∵AC2=DCEC,∴![]() .
.
∵∠ACD=∠ECA,∴△ACD∽△ECA,∴∠ADC=∠EAC=90°,∴∠FDA=∠FAC=90°.
又∵∠AFD=∠CFA,∴△AFD∽△CFA,∴AD:AF=AC:FC.


科目:初中数学 来源: 题型:
【题目】为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小明喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小明从中随机抽取一张卡片是足球社团B的概率是 .
(2)小明先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团D的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
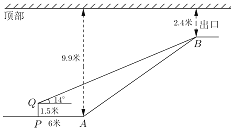
【题目】地铁10号线某站点出口横截面平面图如图所示,电梯![]() 的两端分别距顶部9.9米和2.4米,在距电梯起点
的两端分别距顶部9.9米和2.4米,在距电梯起点![]() 端6米的
端6米的![]() 处,用1.5米的测角仪测得电梯终端
处,用1.5米的测角仪测得电梯终端![]() 处的仰角为14°,求电梯
处的仰角为14°,求电梯![]() 的坡度与长度.(参考数据:
的坡度与长度.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,弦
的直径,弦![]() ,
,![]()
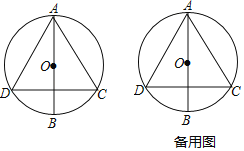
(1)求证:![]() 是等边三角形.
是等边三角形.
(2)若点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,若
,若![]() ,求线段
,求线段![]() 的长;
的长;
(3)若![]() 的半径为4,点
的半径为4,点![]() 是弦
是弦![]() 的中点,点
的中点,点![]() 是直线
是直线![]() 上的任意一点,将点
上的任意一点,将点![]() 绕点
绕点![]() 逆时针旋转60°得点
逆时针旋转60°得点![]() ,求线段
,求线段![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() ,
,![]() 为
为![]() 上一点,过点
上一点,过点![]() 作
作![]() 的弦
的弦![]() ,设
,设![]() .
.
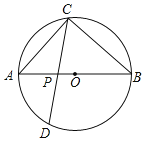
(1)若![]() 时,求
时,求![]() 、
、![]() 的度数各是多少?
的度数各是多少?
(2)当![]() 时,是否存在正实数
时,是否存在正实数![]() ,使弦
,使弦![]() 最短?如果存在,求出
最短?如果存在,求出![]() 的值,如果不存在,说明理由;
的值,如果不存在,说明理由;
(3)在(1)的条件下,且![]() ,求弦
,求弦![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在梯形ABCD中,![]() ,P是线段BC上一点,以P为圆心,PA为半径的
,P是线段BC上一点,以P为圆心,PA为半径的![]() 与射线AD的另一个交点为Q,射线PQ与射线CD相交于点E,设
与射线AD的另一个交点为Q,射线PQ与射线CD相交于点E,设![]() .
.
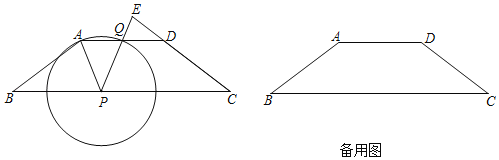
(1)求证:![]() ;
;
(2)如果点Q在线段AD上(与点A、D不重合),设![]() 的面积为y,求y关于x的函数关系式,并写出定义域;
的面积为y,求y关于x的函数关系式,并写出定义域;
(3)如果![]() 与
与![]() 相似,求BP的长.
相似,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在海湾森林公园放风筝.如图所示,小明在A处,风筝飞到C处,此时线长BC为40米,若小明双手牵住绳子的底端B距离地面1.5米,从B处测得C处的仰角为60°,求此时风筝离地面的高度CE.(计算结果精确到0.1米,![]() ≈1.732)
≈1.732)
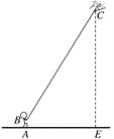
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2﹣x+c的对称轴为直线x=1,与x轴的一个交点为A(﹣1,0),顶点为B.点C(5,m)在抛物线上,直线BC交x轴于点E.
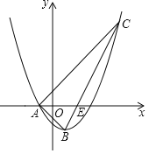
(1)求抛物线的表达式及点E的坐标;
(2)联结AB,求∠B的正切值;
(3)点G为线段AC上一点,过点G作CB的垂线交x轴于点M(位于点E右侧),当△CGM与△ABE相似时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绿色出行是对环境影响最小的出行方式,“共享单车”已成为北京的一道靓丽的风景线.某社会实践活动小
组为了了解“共享单车”的使用情况,对本校教师在3月6日至3月10日使用单车的情况进行了问卷调查,
以下是根据调查结果绘制的统计图的一部分:
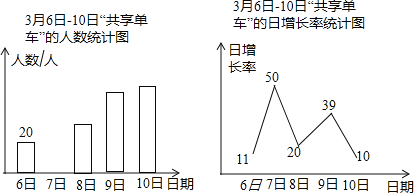
请根据以上信息解答下列问题:
(1)3月7日使用“共享单车”的教师人数为人,并请补全条形统计图;
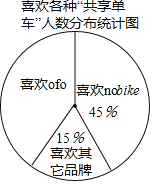
(2)不同品牌的“共享单车”各具特色,社会实践活动小组针对有过使用“共享单车”经历的教师做了进一步调查,每位教师都按要求选择了一种自己喜欢的“共享单车”,统计结果如图,其中喜欢![]() 的教师有36人,求喜欢
的教师有36人,求喜欢![]() 的教师的人数.
的教师的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com