
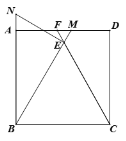
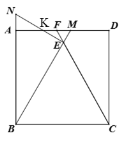
【题目】如图,矩形![]() 中,
中,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,![]() ,则
,则![]() =_________.
=_________.
【答案】![]()
【解析】
通过四边形ABCD是矩形以及![]() ,得到△FEM是等边三角形,根据含30°直角三角形的性质以及勾股定理得到KM,NK,KE的值,进而得到NE的值,再利用30°直角三角形的性质及勾股定理得到BN,BE即可.
,得到△FEM是等边三角形,根据含30°直角三角形的性质以及勾股定理得到KM,NK,KE的值,进而得到NE的值,再利用30°直角三角形的性质及勾股定理得到BN,BE即可.
解:如图,设NE交AD于点K,
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,
∴∠MFE=∠FCB,∠FME=∠EBC
∵![]() ,
,
∴△BCE为等边三角形,
∴∠BEC=∠ECB=∠EBC=60°,
∵∠FEM=∠BEC,
∴∠FEM=∠MFE=∠FME=60°,
∴△FEM是等边三角形,FM=FE=EM=2,
∵EN⊥BE,
∴∠NEM=∠NEB=90°,
∴∠NKA=∠MKE=30°,
∴KM=2EM=4,NK=2AN=6,
∴在Rt△KME中,KE=![]() ,
,
∴NE=NK+KE=6+![]() ,
,
∵∠ABC=90°,
∴∠ABE=30°,
∴BN=2NE=12+![]() ,
,
∴BE=![]() ,
,
∴BC=BE=![]() ,
,
故答案为:![]()


科目:初中数学 来源: 题型:
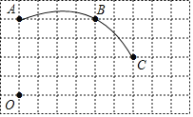
【题目】如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
(1)请完成如下操作:
①以点O为原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,在图中标出该圆弧所在圆的圆心D.
(2)请在(1)的基础上,完成下列填空:
①写出点的坐标:D( );
②⊙D的半径= (结果保留根号);
③利用网格试在图中找出格点E ,使得直线EC与⊙D相切(写出所有可能的结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点
匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点![]() 运动的时间是
运动的时间是![]() 秒
秒![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .
.
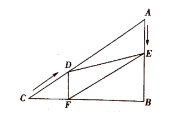
(1)求证:![]() ;
;
(2)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值,如果不能,说明理由:
值,如果不能,说明理由:
(3)当![]() 为何值时,
为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宝安区的某商场经市场调查,预计一款夏季童装能获得市场青睐,便花费 15000 元购进了一批此款童装,上市后很快售罄.该店决定继续进货,由于第二批进货数量是第一批进货数量的 2 倍,因此单价便宜了 10 元,购进第二批童装一共花费了 27000 元.
(1)该店所购进的第一批童装的单价是多少元?
(2)两批童装按相同标价出售,经理根据市场情况,决定对第二批剩余的 100 件打七折销售.若两批童装全部售完后,利润不低于 30%,那么每件童装标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为从小明和小刚中选出一人去观看元旦文艺汇演,现设计了如下游戏,规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P从原点O出发,沿x轴向右以每秒1个单位长的速度运动t(t>0)秒,抛物线![]() 经过点O和点P.已知矩形ABCD的三个顶点为A(1,0),B(1,4),D(4,0).
经过点O和点P.已知矩形ABCD的三个顶点为A(1,0),B(1,4),D(4,0).
(1)求c,b(可用含t的代数式表示);
(2)当t>1时,抛物线与线段![]() 交于点M,交x轴于点E.在点P的运动过程中,你认为∠AMP的大小是否会变化?若变化,说明理由;若不变,求出∠AMP的值;
交于点M,交x轴于点E.在点P的运动过程中,你认为∠AMP的大小是否会变化?若变化,说明理由;若不变,求出∠AMP的值;
(3)点P为x正半轴上的动点,线段PM与线段BC有公共点时,求点P的横坐标t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
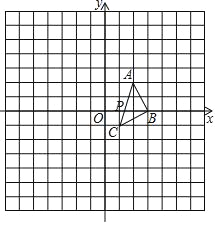
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(3,0),C(1,﹣1),AC交x轴于点P.
(1)∠ACB的度数为_____;
(2)P点坐标为______;
(3)以点O为位似中心,将△ABC放大为原来的2倍,请在图中画出所有符合条件的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校将开启“大阅读”活动,为了充实书吧藏书,学生会号召全年级学生捐书,得到各班的大力支持.同时,年级部分备课组的老师也购买藏书充实到年级书吧,其中数学组购买了甲、乙两种自然科学书籍若干本,用去699元;语文组购买了A、B两种文学书籍若干本,用去6138元,已知A、B的数量分别与甲、乙的数量相等,且甲种书与B种书的单价相同,乙种书与A种书的单价相同,若甲种书的单价比乙种书的单价多7元,则乙种书籍比甲种书籍多买了_____本.
.
查看答案和解析>>
科目:初中数学 来源: 题型:
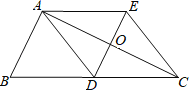
【题目】如图,已知△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,联结EC.
(1)求证:四边形ADCE是平行四边形;
(2)当∠BAC=90°时,求证:四边形ADCE是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com