
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,��P��ԭ��O����,��x��������ÿ��1����λ�����ٶ��˶�t(t>0)��,������![]() ������O�͵�P.��֪����ABCD����������ΪA(1,0),B(1,4),D(4,0).
������O�͵�P.��֪����ABCD����������ΪA(1,0),B(1,4),D(4,0).
��1����c,b(���ú�t�Ĵ���ʽ��ʾ)��
��2����t>1ʱ�����������߶�![]() ���ڵ�M����x���ڵ�E.�ڵ�P���˶������У�����Ϊ��AMP�Ĵ�С�Ƿ��仯?���仯��˵�����ɣ������䣬�����AMP��ֵ��
���ڵ�M����x���ڵ�E.�ڵ�P���˶������У�����Ϊ��AMP�Ĵ�С�Ƿ��仯?���仯��˵�����ɣ������䣬�����AMP��ֵ��
��3����PΪx�������ϵĶ��㣬�߶�PM���߶�BC�й�����ʱ�����P�ĺ�����t��ȡֵ��Χ.

���𰸡�(1) b=t��(2) ��������EMP=45�㣻��3�����߶�PM���߶�BC�й�����ʱ����P�ĺ�����t ��ȡֵ��ΧΪ5�Qt�Q8.
��������
��1����������y=x2+bx+c������O�͵�P������O��P��������뷽�̼������c��b��
��2����x=-1ʱ��y=-1-t�����M�����꣬�����á�AMP�Ķ�����
��3����ֱ��PM�Ľ���ʽΪ![]() ��P(t��0������M��-1��-1-t��������⣬�ٸ����߶�PM���߶�BC�й����������Χ��
��P(t��0������M��-1��-1-t��������⣬�ٸ����߶�PM���߶�BC�й����������Χ��
(1)��x=0,y=0����![]() ����c=0��
����c=0��
�ٰ�x=t,y=0����![]() ,��
,��![]() ��
��
��t>0��
��b=t��
(2)���䡣
�������ߵĽ���ʽΪ��![]() ����M�ĺ�����Ϊ1��
����M�ĺ�����Ϊ1��
�൱x=-1ʱ��y=-1t��
��M(-1,-1t)��
��EM=t+1��EP=t+1
��EM=EP��
�ߡ�PEM=90����
���EMP=45����
��3����ֱ��PM�Ľ���ʽΪ![]() ��m��0��
��m��0��
��ֱ��PM������P(t��0������M��-1��-1-t��
![]()
![]()
M=1��n=-t
��ֱ��PM�Ľ���ʽΪ![]()
��PM����B��1��-4��ʱ����1-t=-4�����t=5
��PM����C,(4,-4)ʱ����4-t=-4�����t=8
�൱�߶�PM���߶�BC�й�����ʱ����P�ĺ�����t ��ȡֵ��ΧΪ5�Qt�Q8.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��O��ֱ��AB�ij�Ϊ10����AC�ij�Ϊ5����ACB��ƽ���߽�O�ڵ�D.

��1������ADC�Ķ�����
��2������BD�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ��� y��ax+bx+c��a��0����ͼ����ͼ��ʾ��A���� 1��3���������ߵĶ��㣬�����½�������ȷ���ǣ� ��
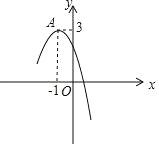
A. a��0��b��0��c��0
B. 2a+b��0
C. �� x��0 ʱ��y �� x ���������С
D. ax2+bx+c��3��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
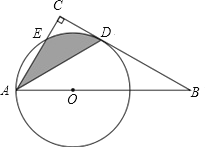
����Ŀ����ͼ����C=90�㣬��OΪRt��ABCб��AB�ϵ�һ�㣬��OAΪ�뾶�ġ�O���BC���ڵ�D�����AC���ڵ�E������AD����ADƽ�֡�BAC.
��1����֤��BC�ǡ�O�����ߣ�
��2������BAC=60��,OA=1,����Ӱ���ֵ����(���������).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�
�У�![]() ���ӳ�
���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ���ӳ�
���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ����
����![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��
��![]() ����
����![]() =_________��
=_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
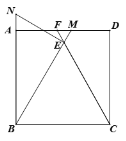
����Ŀ����ͼ��������![]() �У�
��![]() ��
��![]() �Ĵ�ֱƽ���߽��Խ���
�Ĵ�ֱƽ���߽��Խ���![]() �ڵ�
�ڵ�![]() ,
,![]() Ϊ���㣬����
Ϊ���㣬����![]() ����
����![]() ���ڣ� ��
���ڣ� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�����Ҫ����
��ģ�ͽ��ܣ�
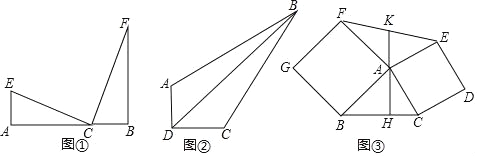
��ͼ����C���߶�A��B��һ��E��F��ABͬ�࣬�ҡ�A����B����ECF��90��������ȥ��һ����K�������dz�ͼ��Ϊ��K����ͼ��
������̽����
����1����ͼ�٣���EC��FC����ACE�ա�BFC
����2����ͼ�٣���EC��FC����ACE����BFC�����ƱȲ�Ϊ1��
��ģ��Ӧ�ã�
Ӧ��1����ͼ�ڣ����ı���ABCD�У���ADC��90�㣬AD��1��CD��2��BC��2![]() ��AB��5����BD��
��AB��5����BD��
Ӧ��2����ͼ�ۣ���֪��ABC���ֱ���AB��ACΪ��������������ABGF��������ACDE��AH��BC������EF����AH�ķ����ӳ����ڵ�K��֤����KΪEF�е㣮
��1�������������1��֤�����̣�
��2����ֱ���Ӧ��1��Ӧ��2��������⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ʣ�������������������Ϊ�ļ�֮ˮ��������ζ���ܽ���ȥ����Ӻ��ͣ�������DzʳƷ����Ƥҩ�ã������ȡ�����Ѫѹ֮Ч.ij���������̴��㹺���������ˡ������롰���ѡ���������Ʒ�ֵ����Ϲ�70000ǧ�ˣ�
��1���������������ˡ����ϵ����������������ѡ�����������![]() ���������ˡ�������������ǧ�ˣ�
���������ˡ�������������ǧ�ˣ�
��2���������̰���1���С������ˡ������������������Ԥ�ơ������ˡ������ۼ�Ϊ4Ԫ/ǧ�ˣ������ѡ������ۼ�Ϊ5Ԫ/ǧ�ˣ���������ȫ������.���ڴ洢������Ӱ�죬�������ˡ������롰���ѡ����Ϸֱ���![]() ��
��![]() ���������۳�.���������ȣ������������������ˡ����ϵ����ۼ۸�����
���������۳�.���������ȣ������������������ˡ����ϵ����ۼ۸�����![]() �������ѡ����ϵ����ۼ۸�����
�������ѡ����ϵ����ۼ۸�����![]() ���������֮�����õ������۶��ԭ�ƻ��½���3000Ԫ����
���������֮�����õ������۶��ԭ�ƻ��½���3000Ԫ����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=k1x+b��ͼ��A��0����2����B��1��0�����㣬�뷴��������![]() ��ͼ���ڵ�һ�����ڵĽ���ΪM������OBM�����Ϊ2��
��ͼ���ڵ�һ�����ڵĽ���ΪM������OBM�����Ϊ2��
��1����һ�κ����ͷ����������ı���ʽ��
��2����x�����Ƿ���ڵ�P��ʹAM��MP�������ڣ������P�����ꣻ�������ڣ�˵�����ɣ�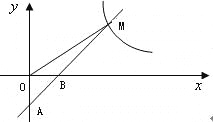
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com