
【题目】宝安区的某商场经市场调查,预计一款夏季童装能获得市场青睐,便花费 15000 元购进了一批此款童装,上市后很快售罄.该店决定继续进货,由于第二批进货数量是第一批进货数量的 2 倍,因此单价便宜了 10 元,购进第二批童装一共花费了 27000 元.
(1)该店所购进的第一批童装的单价是多少元?
(2)两批童装按相同标价出售,经理根据市场情况,决定对第二批剩余的 100 件打七折销售.若两批童装全部售完后,利润不低于 30%,那么每件童装标价至少是多少元?
【答案】(1)该店所购进的第一批童装的单价是 100 元/件;(2)每件童装标价至少为 130 元.
【解析】
1)设该店所购进的第一批童装的单价是 x 元/件,则该店所购进的第二批童装的单价是(x﹣10)元/件,根据数量=总价÷单价结合于第二批进货数量是第一批进货数量的 2 倍,即可得出关于 x 的分式方程,解之经检验后即可得出结论;
(2)根据数量=总价÷单价可求出第一批购进的数量,用其×2 可得出第二批购进的数量,设每件童装标价为 y 元,根据利润=销售收入﹣成本,即可得出关于 y 的一元一次不等式,解之取其中的最小值即可得出结论.
(1)设该店所购进的第一批童装的单价是 x 元/件,则该店所购进的第二批童装的单价是(x﹣10)元/件,
根据题意得:![]() ,
,
解得:x=100,
经检验,x=100 是原分式方程的解且符合题意. 答:该店所购进的第一批童装的单价是 100 元/件.
(2)第一批购进的数量为 15000÷100=150(件),第二批购进的数量为 150×2=300(件).
设每件童装标价为 y 元,
根据题意得:(150+300﹣100)y+100×0.7y﹣15000﹣27000≥(15000+27000)×30%,
解得:y≥130.
答:每件童装标价至少为 130 元.


科目:初中数学 来源: 题型:
【题目】小强骑车从家到学校要经过一段先上坡后下坡的路,在这段路上小强骑车的距离s(千米)与骑车的时间t(分钟)之间的函数关系如图所示,请根据图中信息回答下列问题:
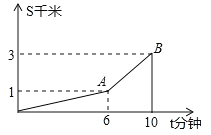
(1)小强去学校时下坡路长 千米;
(2)小强下坡的速度为 千米/分钟;
(3)若小强回家时按原路返回,且上坡的速度不变,下坡的速度也不变,那么回家骑车走这段路的时间是 分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数 y=ax+bx+c(a≠0)的图象如图所示,A(﹣ 1,3)是抛物线的顶点,则以下结论中正确的是( )
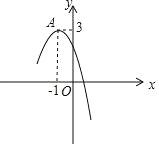
A. a<0,b>0,c>0
B. 2a+b=0
C. 当 x<0 时,y 随 x 的增大而减小
D. ax2+bx+c﹣3≤0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠BAC=90°,分别以 AC 和 BC 为边向外作正方形 ACFG 和正方形 BCDE,过点 D 做 FC 的延长线的垂线,垂足为点 H.
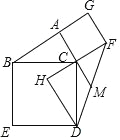
(1)求证:△ABC≌△HDC;
(2)连接 FD,交 AC 的延长线于点 M,若 AG=![]() ,tan∠ABC=
,tan∠ABC= ![]() ,求△FCM 的面积.
,求△FCM 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
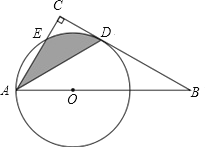
【题目】如图,∠C=90°,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与边BC交于点D,与边AC交于点E,连接AD,且AD平分∠BAC.
(1)求证:BC是⊙O的切线;
(2)若∠BAC=60°,OA=1,求阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并按要求解答.
(模型介绍)
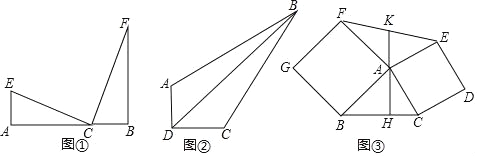
如图①,C是线段A、B上一点E、F在AB同侧,且∠A=∠B=∠ECF=90°,看上去像一个“K“,我们称图①为“K”型图.
(性质探究)
性质1:如图①,若EC=FC,△ACE≌△BFC
性质2:如图①,若EC≠FC,△ACE~△BFC且相似比不为1.
(模型应用)
应用1:如图②,在四边形ABCD中,∠ADC=90°,AD=1,CD=2,BC=2![]() ,AB=5.求BD.
,AB=5.求BD.
应用2:如图③,已知△ABC,分别以AB、AC为边向外作正方形ABGF、正方形ACDE,AH⊥BC,连接EF.交AH的反向延长线于点K,证明:K为EF中点.
(1)请你完成性质1的证明过程;
(2)请分别解答应用1,应用2提出的问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
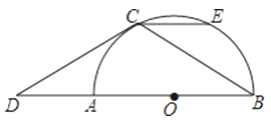
【题目】如图,AB是半圆O的直径,点C在半圆上,过点C的切线交BA的延长线于点D,CD=CB,CE∥AB交半圆于点E.
(1)求∠D的度数;
(2)求证:以点C,O,B,E为顶点的四边形是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com