
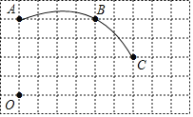
【题目】如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
(1)请完成如下操作:
①以点O为原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,在图中标出该圆弧所在圆的圆心D.
(2)请在(1)的基础上,完成下列填空:
①写出点的坐标:D( );
②⊙D的半径= (结果保留根号);
③利用网格试在图中找出格点E ,使得直线EC与⊙D相切(写出所有可能的结果).
【答案】(1)见解析;(2)①(2,0);②2![]() ;③(7,0).
;③(7,0).
【解析】
(1)根据题意建立平面直角坐标系,然后作出弦AB的垂直平分线,以及BC的垂直平分线,两直线的交点即为圆心D,连接AD,CD;
(2)①根据第一问画出的图形即可得出D的坐标;
②在直角三角形AOD中,由OA及OD的长,利用勾股定理求出AD的长,即为圆D的半径;
③根据半径相等得出CD=AD=2![]() ,设EF=x,在Rt△CDE和Rt△CEF中,根据勾股定理列出两个式子即可求出x的值,从而求出E点坐标
,设EF=x,在Rt△CDE和Rt△CEF中,根据勾股定理列出两个式子即可求出x的值,从而求出E点坐标
(1)根据题意画出相应的图形,如图所示:
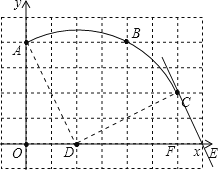
(2)①根据图形得:D(2,0);
②在Rt△AOD中,OA=4,OD=2,
根据勾股定理得:AD=![]() =2
=2![]()
则D的半径为2![]()
③∵EC与⊙D相切
∴CE⊥DC
∴△CDE为直角三角形即∠DCE=90°
∵AD和CD都是圆D的半径,
∴由②知,CD=AD=2![]()
设EF=x
在Rt△CDE中,(2![]() )2+CE2=(4+x)2
)2+CE2=(4+x)2
在Rt△CEF中,22+x2=CE2
∴(2![]() )2+(22+x2)=(4+x)2
)2+(22+x2)=(4+x)2
解得,x=1,即EF=1
∴OE=2+4+1=7
∴E点坐标为(7,0)


科目:初中数学 来源: 题型:
【题目】(本题满分10分)在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票原定的票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠措施,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强骑车从家到学校要经过一段先上坡后下坡的路,在这段路上小强骑车的距离s(千米)与骑车的时间t(分钟)之间的函数关系如图所示,请根据图中信息回答下列问题:
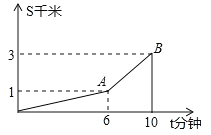
(1)小强去学校时下坡路长 千米;
(2)小强下坡的速度为 千米/分钟;
(3)若小强回家时按原路返回,且上坡的速度不变,下坡的速度也不变,那么回家骑车走这段路的时间是 分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初二数学兴趣小组活动时,碰到这样一道题:
“已知正方形AD,点E、F、G、H分别在边AB、BC、CD、DA上,若![]() ,则EG=FH”.
,则EG=FH”.
经过思考,大家给出了以下两个方案:
(甲)过点A作AM∥HF交BC于点M,过点B作BN∥EG交CD于点N;
(乙)过点A作AM∥HF交BC于点M,作AN∥EG交CD的延长线于点N;
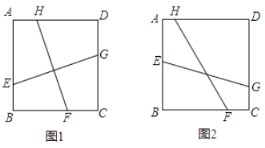
(1)对小杰遇到的问题,请在甲、乙两个方案中任选一个,加以证明(如图1)
(2)如果把条件中的“![]() ”改为“EG与FH的夹角为45°”,并假设正方形ABCD的边长为1,FH的长为
”改为“EG与FH的夹角为45°”,并假设正方形ABCD的边长为1,FH的长为![]() (如图2),试求EG的长度.
(如图2),试求EG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市城建公司新建了一个购物中心,共有商铺30间,据调查分析,当每间的年租金为10万元时,可全部租出:若每间的年租金每增加0.5万元,则少租出商铺一间,为提供优质服务,城建公司引入物业公司代为管理,租出的商铺每间每年需向物业公司缴纳物业费1万元,未租出的商铺不需要向物业公司缴纳物业费.
(1)当每间商铺的年租金定为13万元时,能租出 间.
(2)当每问商铺的年租金定为多少万元时,该公司的年收益为286万元,且使租客获得实惠?(收益=租金﹣物业费)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com