
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点
匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点![]() 运动的时间是
运动的时间是![]() 秒
秒![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .
.
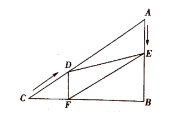
(1)求证:![]() ;
;
(2)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值,如果不能,说明理由:
值,如果不能,说明理由:
(3)当![]() 为何值时,
为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.
【答案】(1)见详解;(2)能,![]() ;(3)
;(3)![]() 或
或![]() ,见详解
,见详解
【解析】
(1)利用t表示出CD和AE的长,然后在直角![]() 中,利用直角三角形的性质求得DF的长,即可证明;
中,利用直角三角形的性质求得DF的长,即可证明;
(2)先证明四边形AEFD是平行四边形,当![]() 时,四边形AEFD是菱形,据此列出方程求得t值.
时,四边形AEFD是菱形,据此列出方程求得t值.
(3)分别从![]() 和
和![]() 两种情况分类讨论即可.
两种情况分类讨论即可.
解:(1)证明:![]() 中,
中,![]() ,
,![]() ,
,
![]() .
.
∵![]() ,
,
∴![]()
![]() 在
在![]() 中,
中,![]()
∵![]() ,
,![]() ,
,
∴![]()
![]()
(2)![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
当![]() 时,四边形
时,四边形![]() 是菱形,
是菱形,
即![]() ,解得:
,解得:![]() ,
,
即当![]() 时,平行四边形
时,平行四边形![]() 是菱形;
是菱形;
(3)当![]() 时,
时,![]() 是直角三角形
是直角三角形![]() ;或
;或
当![]() 时,
时,![]() 是直角三角形
是直角三角形![]()
理由如下:当![]() 时,
时,![]()
![]() ,
,![]() ,
,
即![]()
解得:![]()
![]() 时,
时,![]() .
.![]() 是直角三角形
是直角三角形
当![]() 时,
时,![]() .
.
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]()
![]()
![]() 是直角三角形,
是直角三角形,![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,解得
,解得![]() .
.
综上所述,当![]() 时
时![]() 是直角三角形
是直角三角形![]() ;
;
当![]() 时,
时,![]() 也是直角三角形.
也是直角三角形.![]()


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】我市城建公司新建了一个购物中心,共有商铺30间,据调查分析,当每间的年租金为10万元时,可全部租出:若每间的年租金每增加0.5万元,则少租出商铺一间,为提供优质服务,城建公司引入物业公司代为管理,租出的商铺每间每年需向物业公司缴纳物业费1万元,未租出的商铺不需要向物业公司缴纳物业费.
(1)当每间商铺的年租金定为13万元时,能租出 间.
(2)当每问商铺的年租金定为多少万元时,该公司的年收益为286万元,且使租客获得实惠?(收益=租金﹣物业费)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
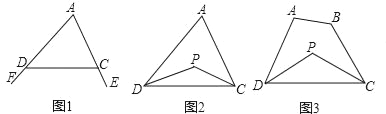
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数 y=ax+bx+c(a≠0)的图象如图所示,A(﹣ 1,3)是抛物线的顶点,则以下结论中正确的是( )
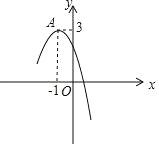
A. a<0,b>0,c>0
B. 2a+b=0
C. 当 x<0 时,y 随 x 的增大而减小
D. ax2+bx+c﹣3≤0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠BAC=90°,分别以 AC 和 BC 为边向外作正方形 ACFG 和正方形 BCDE,过点 D 做 FC 的延长线的垂线,垂足为点 H.
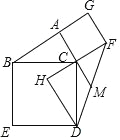
(1)求证:△ABC≌△HDC;
(2)连接 FD,交 AC 的延长线于点 M,若 AG=![]() ,tan∠ABC=
,tan∠ABC= ![]() ,求△FCM 的面积.
,求△FCM 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 、
、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点.点
两点.点![]() 为线段
为线段![]() 的中点.过点
的中点.过点![]() 作直线
作直线![]() 轴于点
轴于点![]() .
.
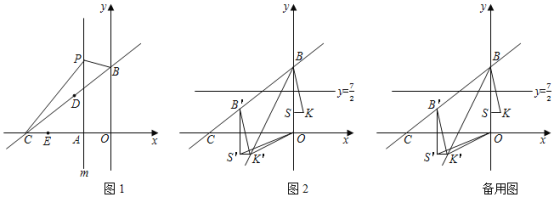
(1)直接写出![]() 的坐标;
的坐标;
(2)如图1,点![]() 是直线
是直线![]() 上的动点,连接
上的动点,连接![]() 、
、![]() ,线段
,线段![]() 在直线
在直线![]() 上运动,记为
上运动,记为![]() ,点
,点![]() 是
是![]() 轴上的动点,连接点
轴上的动点,连接点![]() 、
、![]() ,当
,当![]() 取最大时,求
取最大时,求![]() 的最小值;
的最小值;
(3)如图2,在![]() 轴正半轴取点
轴正半轴取点![]() ,使得
,使得![]() ,以
,以![]() 为直角边在
为直角边在![]() 轴右侧作直角
轴右侧作直角![]() ,
,![]() ,且
,且![]() ,作
,作![]() 的角平分线
的角平分线![]() ,将
,将![]() 沿射线
沿射线![]() 方向平移,点
方向平移,点![]() 、
、![]() ,
,![]() 平移后的对应点分别记作
平移后的对应点分别记作![]() 、
、![]() 、
、![]() ,当
,当![]() 的点
的点![]() 恰好落在射线
恰好落在射线![]() 上时,连接
上时,连接![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 沿顺时针方向旋转
沿顺时针方向旋转![]() 后得
后得![]() ,在直线
,在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 为等腰三角形?若存在,请直接写出点
为等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com