
【题目】如图,AB为☉O的直径,CD与☉O相切于点E,交AB的延长线于点D,连接BE,过点O作OC∥BE,交☉O于点F,交切线于点C,连接AC.
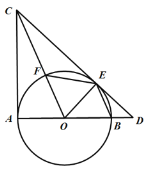
(1)求证:AC是☉O的切线;
(2)连接EF,当∠D= °时,四边形FOBE是菱形.
【答案】(1)详见解析;(2)30.
【解析】
(1)利用切线的性质得∠CEO=90°,再证明△OCA≌△OCE得到∠CAO=∠CEO=90°,然后根据切线的判定定理得到结论;
(2)利用四边形FOBE是菱形得到OF=OB=BF=EF,则可判定△OBE为等边三角形,所以∠BOE=60°,然后利用互余可确定∠D的度数.
(1)证明:∵CD与⊙O相切于点E,
∴OE⊥CD,
∴∠CEO=90°,
又∵OC∥BE,
∴∠COE=∠OEB,∠OBE=∠COA
∵OE=OB,
∴∠OEB=∠OBE,
∴∠COE=∠COA,
又∵OC=OC,OA=OE,
∴△OCA≌△OCE(SAS),
∴∠CAO=∠CEO=90°,
又∵AB为⊙O的直径,
∴AC为⊙O的切线;
(2)∵四边形FOBE是菱形,
∴OF=OB=BF=EF,
∴OE=OB=BE,
∴△OBE为等边三角形,
∴∠BOE=60°,
而OE⊥CD,
∴∠D=30°.


科目:初中数学 来源: 题型:
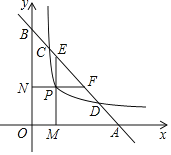
【题目】如图,直线y=﹣x+4分别交x轴、y轴于A、B两点,P是反比例函数y=![]() (x>0),图象上位于直线y=﹣x+4下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于点F,并且AFBE=4
(x>0),图象上位于直线y=﹣x+4下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于点F,并且AFBE=4
(1)求k的值;
(2)若反比例函数y=![]() 与一次函数y=﹣x+4交于C、D两点,求三角形OCD的面积.
与一次函数y=﹣x+4交于C、D两点,求三角形OCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强学生体质,某校对学生设置了体操、球类、跑步、游泳等课外体育活动,为了了解学生对这些项目的喜爱情况,在全校范围内随机抽取了若干名学生,对他们最喜爱的体育项目(每人只选一项)进行了问卷调查,将数据进行了统计并绘制成了如图所示的频数分布直方图和扇形统计图(均不完整).
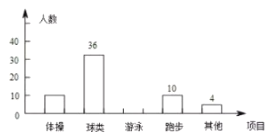
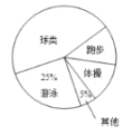
(1)在这次问卷调查中,一共抽查了多少名学生?
(2)补全频数分布直方图,求出扇形统计图中“体操”所对应的圆心角度数;
(3)估计该校![]() 名学生中有多少人喜爱跑步项目.
名学生中有多少人喜爱跑步项目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:P(1,0)、Q(2,﹣2)都是“整点”.抛物线y=mx2﹣4mx+4m﹣2(m>0)与x轴交于A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】许昌芙蓉湖位于许昌市水系建设总体规划中部,上游接纳清泥河来水,下游为鹿鸣湖等水系供水,承担着承上启下的重要作用,是利用有限的水资源、形成良好的水生态环境打造生态宜居城市的重要部分.某校课外兴趣小组想测量位于芙蓉湖两端的A,B两点之间的距离他沿着与直线AB平行的道路EF行走,走到点C处,测得∠ACF=45°,再向前走300米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为200米,求A,B两点之间的距离(结果保留一位小数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一些半径相同的小圆按如图所示的规律摆放,第1个图形有4个小圆,第2个图形有8个小圆,第3个图形有14个小圆,…,依此规律,第9个图形的小圆个数是( )
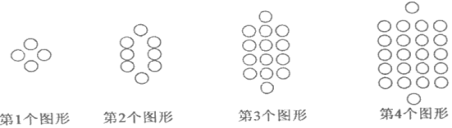
A.58 B.74 C.92 D.112
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个不等实数,我们规定满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数闭区间[m,n]上的“闭函数”.如函数y=﹣x+4.当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”
(1)反比例函数![]() 是闭区间[1,2019]上的“闭函数”吗?请判断并说明理由.
是闭区间[1,2019]上的“闭函数”吗?请判断并说明理由.
(2)若二次函数y=x2﹣2x﹣k是闭区间[1,2]上的“闭函数”,求k的值;
(3)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式(用含m,n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额﹣生产费用)

(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
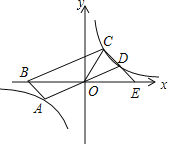
【题目】如图,在平面直角坐标系中,平行四边形ABCD的边AD经过O点,A、C、D三点都在反比例函数y=![]() 的图象上,B点在x轴的负半轴上,延长CD交x轴于点E,连接CO.若S平行四边形ABCD=6,则k的值为_____.
的图象上,B点在x轴的负半轴上,延长CD交x轴于点E,连接CO.若S平行四边形ABCD=6,则k的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com